klasická matematika úzce souvisí s klasickou geometrií v architektuře. Téma, o kterém jsem hovořil v předchozím příspěvku zde. Toto není úplný seznam metod nebo vzorců, ale jednoduchý přehled metod, které architekti používali v minulosti. Za účelem zjednodušení vylučujeme strukturální výpočty, které jsou založeny na materiálech, měřítku a zatížení, a proto jsou příliš široké pro jednoduchý blogový příspěvek.
tradičně používá matematiky
ačkoli jsme se často odkazují na to, jak je v minulosti, stále existuje pokračující tradice klasické architektury, a to jak lidové a klasicismu. Tradiční použití matematiky lze zjednodušit do 4 oblastí:
- strukturální výpočty
- geometrie a prostorové formy
- tvoří estetiku nebo víru v krásu vyplývající z forem; proporcí a symetrií.
- dekorace povrchů a tvarů v prostorovém prostředí
modernismus se od toho v mnoha ohledech odklonil, ale rostoucí zájem o parametrickou architekturu znovu zapálil zájem o matematiku a geometrii v architektuře. To bylo obohaceno v době po kalkulu výpočtem environmentálních a funkčních parametrů. Předmět, který bude prozkoumán v jiném samostatném příspěvku.
strukturální výpočet je podstatným tématem a zde se nebude podrobně zabývat. Stačí říci, že konstrukční návrh se vyvinul z odhadu materiálových kvalit na informovaný výpočet před výstavbou. Oblast nebo architektonická teorie“ hmotné kultury “ teoretizuje, že k architektonickému kulturnímu růstu dochází, když se tradiční konstrukční metoda pohybuje z jednoho materiálu do druhého. Příkladem je klasická západní architektura, která byla původně dřevěná, která byla poté přeložena do kamene. Prvky klasické architektury stále nesou tyto původní dřevěné detaily, nyní používané jako čisté dekorace v kameni. Rozsah a technologie nových materiálových komponent by se přirozeně musely změnit v překladu a vytvořit novou estetiku.
geometrie
zatímco geometrie a prostorové formy jsou odvozeny z matematiky, diskutoval jsem o tom v samostatném příspěvku.
bohové nebo Příroda
příroda a náboženství byly vždy základem v designu našeho prostředí. Rané agrární kultury by zjistily, že příroda dodržovala pravidla, která by mohla být přeložena do matematiky, od proporcionálních pravidel po fraktalizaci až po pojmenování dvou. To bylo bráno jako důkaz toho, že vesmír byl navržen bohy. Bohoslužby by tedy přirozeně musely používat tato „posvátná“ pravidla. Tato pravidla by se pak rozptýlila do jiných míst moci a poté do obecného lidového použití.
náboženské použití těchto matematiky má tendenci být základem symbolického vyjádření zbožného designu, zatímco světské použití bylo více reprezentativní povahy. Použití těchto matematik a geometrií se proto mezi těmito metodami pohybovalo v závislosti na filozofii té doby, s přidělením překrývání.

Zlatý řez / poměr
dvě veličiny s přídělem k sobě, který je stejný jako poměr jejich součtu k většímu množství. Zlatý řez byl považován za základní estetickou formu, kvůli jeho hojnému příkladu v přírodě. Estetická teorie tvrdí, že je to zvláštní krása pochází z formy, která je „mezi“ mezi čtvercem a obdélníkem.
od klasických řeckých chrámů po renesanční kostely a Corbusierovy fasády je to pravděpodobně nejznámější klasický vzorec jak v celkové geometrii, tak v detailech budovy.
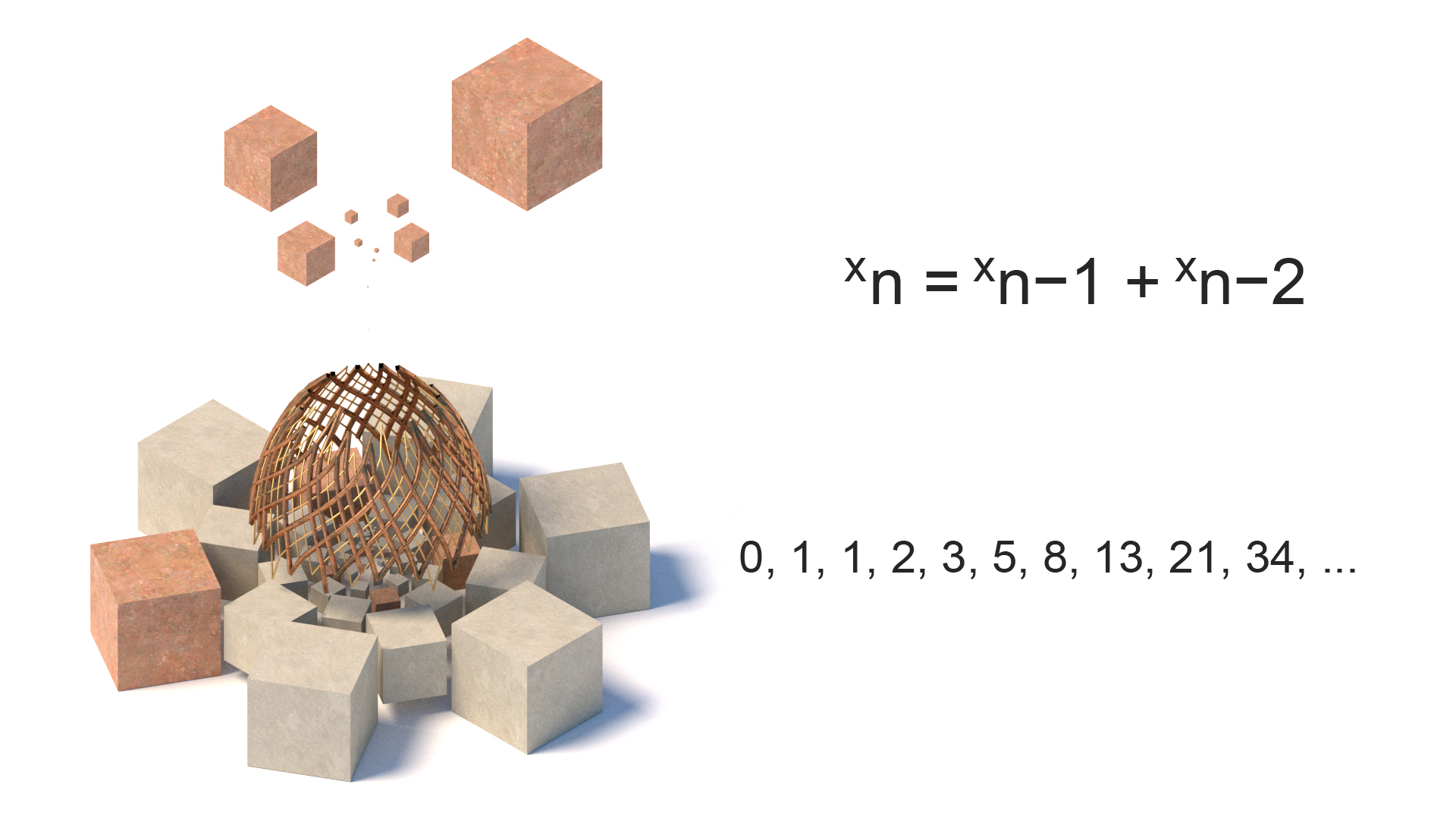
Fibonacciho čísla
pojmenovaná po italském matematikovi Leonardovi z Pisy, Fibonacciho sekvence jsou čísla, kde každé číslo je součtem dvou postupujících čísel. Sekvence, pokud je pozorována často v přírodě, jako je větvení stromů, šišky atd. Použití tohoto ve spirálních formách lze nalézt v čemkoli od klasických řeckých chrámů po Monu Lisu.
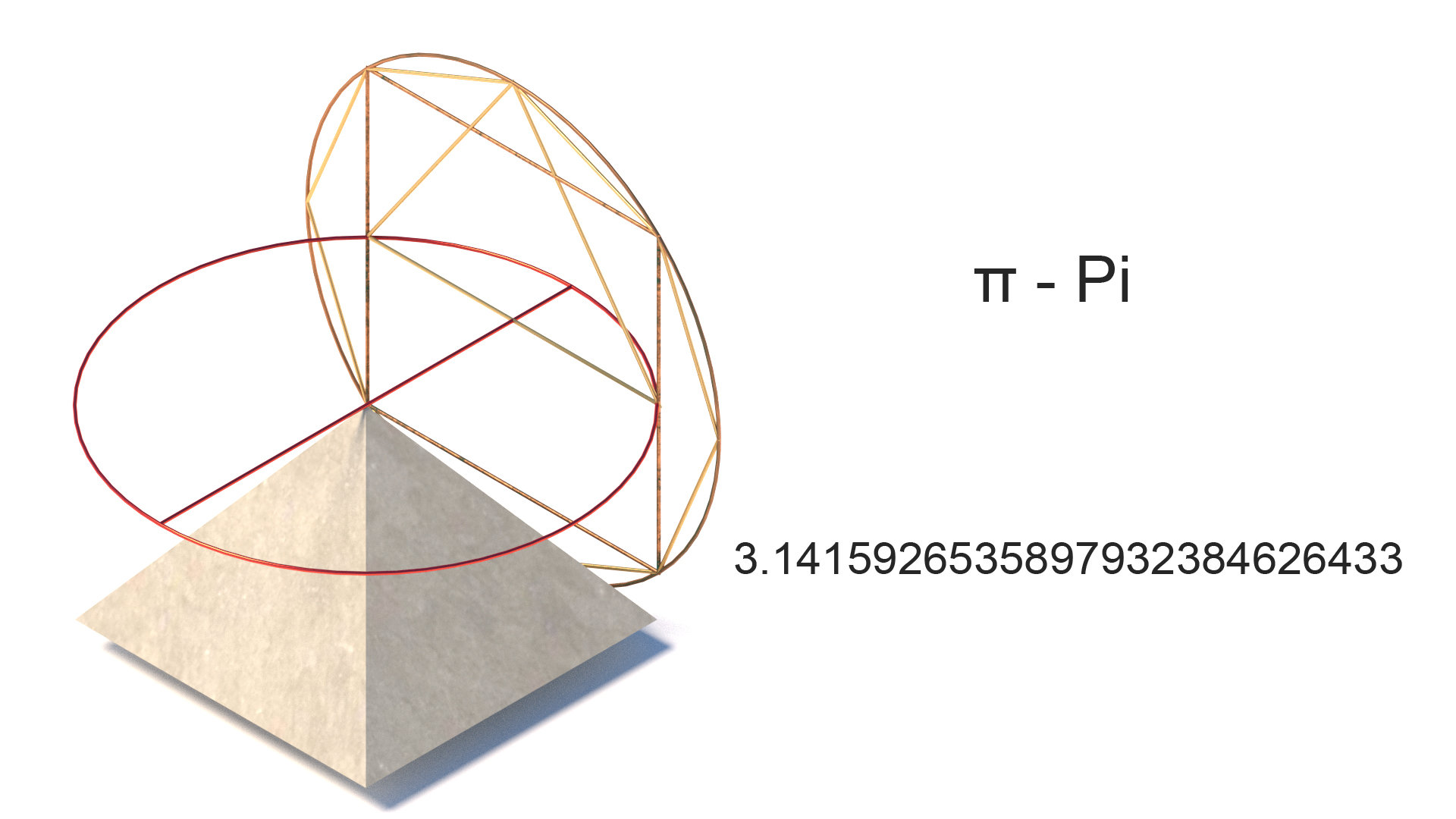
Pi π
Pi je v zásadě poměr obvodu kruhu k jeho průměru a rovná se přibližně 3.14159. Reprezentováno řeckým “ π “ od 18. století. Zatímco pi je užitečné pro „umocnění kruhu“ a výpočet použití kruhových forem, z minulosti byla nalezena jiná použití. John Taylor (1859) zjistil, že pokud je obvod pyramidy dělen jeho výškou, výsledkem je blízká aproximace 2 &pi.
Pi může pomoci měřit věci, jako jsou tekuté, zvukové a světelné vlny, a pravděpodobnost, jako je rozdělení uzlů v současné matematice založené na počtu. Je tedy jádrem mnoha současných parametrických výpočtů.
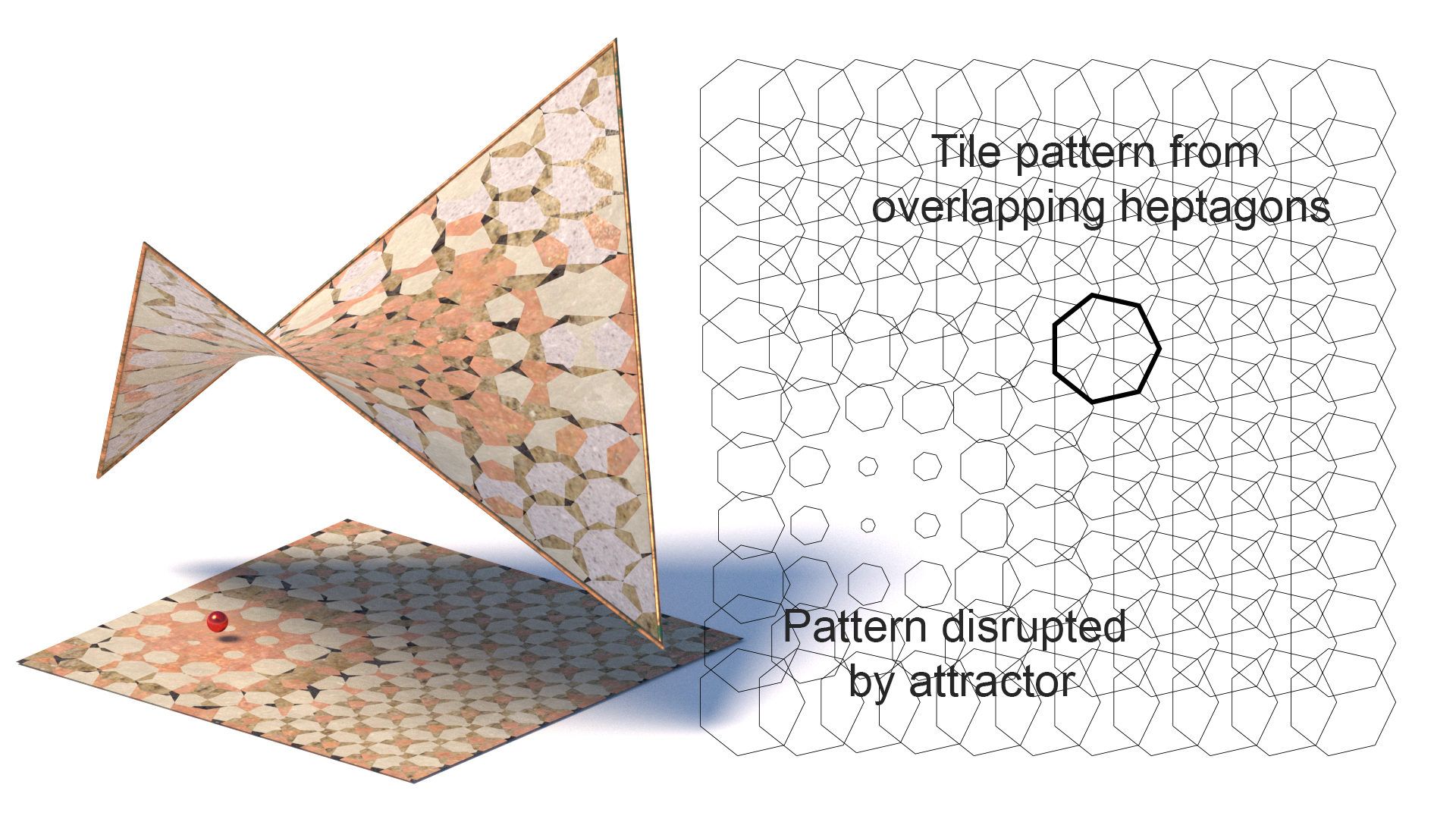
2D a 3D obklady
teselace (obklady)
obklady zahrnovaly pokrývání rovinného povrchu v geometrických tvarech. Nejjednodušší jsou obdélníkové dlaždice, které se často používají v koupelnách a kuchyních. Složitější formy vyžadují složitější metody pro opakující se geometrie. Klasická matematika opakujících se vzorů byla vysoce rozvinutá na Středním východě a v jihovýchodní Asii. Existuje mnoho různých forem tesselations, některé populární patří:
- pravidelné teselace jsou symetrické obklady od okraje k okraji.
- polopravidelná / Archimedovská teselace používá více než jeden typ pravidelného mnohoúhelníku v izogonálním uspořádání
- Monoedrální obklad je teselace, ve které mají všechny dlaždice stejný tvar a velikost.
- Isohedrální obklady jsou speciální variantou monohedrálního obkladu, ve kterém všechny dlaždice patří do stejné třídy tranzitivity
- Voronoi / Dirichlet obkládání jsou teselace, kde každá dlaždice je definována jako sada bodů nejblíže k jednomu z bodů v diskrétní sadě definujících bodů.
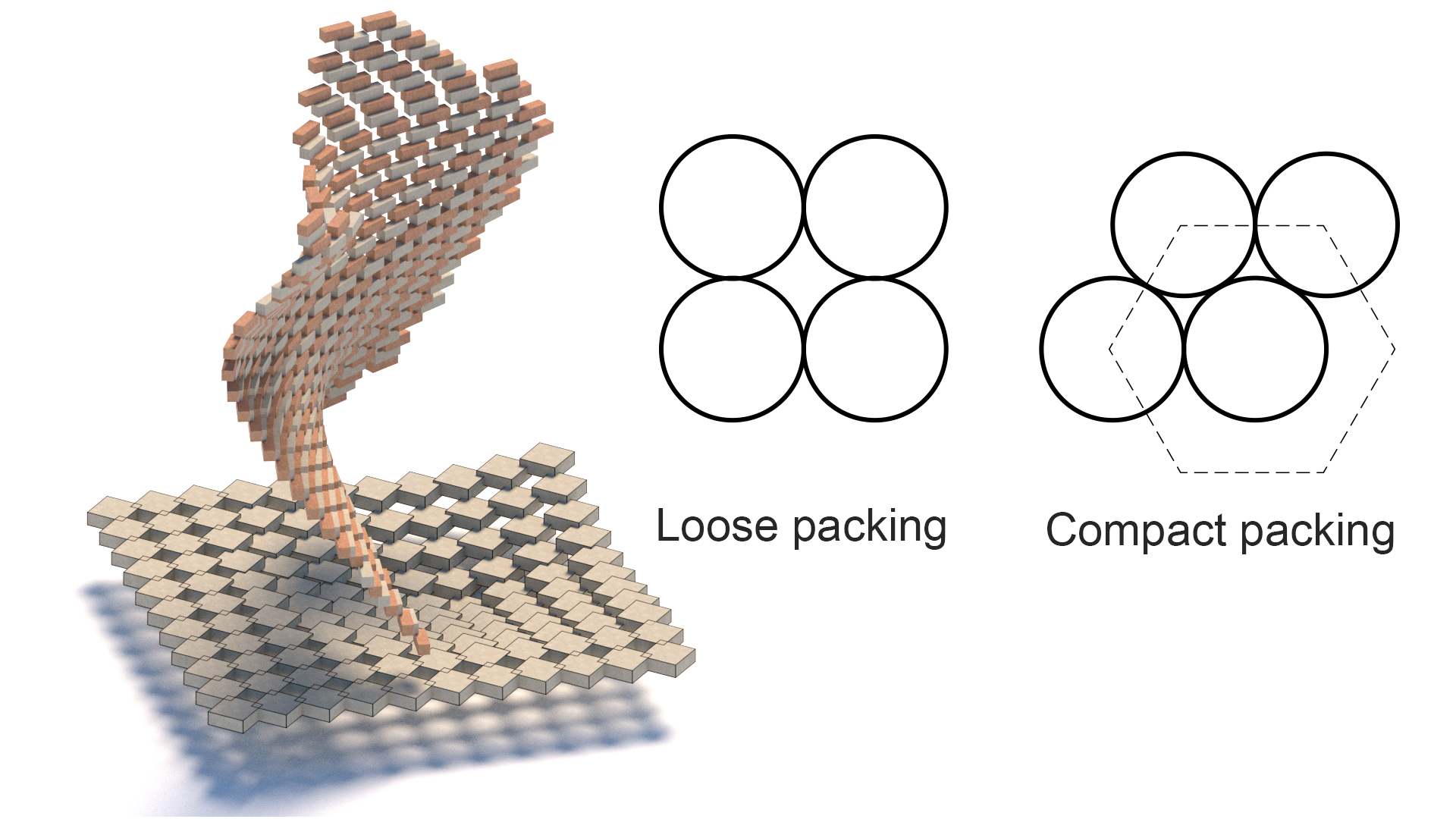
klasická Architektura balení
balení
verze teselace, balení zahrnuje stohování a spojování 3 rozměrových jednotek do koherentního vzoru s různou úrovní hustoty.
problém balení zahrnuje dvě proměnné:
- „kontejnery“; obvykle jedna dvourozměrná nebo trojrozměrná oblast nebo nekonečný prostor
- sada „objektů“, které mají být zabaleny do jednoho nebo více kontejnerů. Sada může obsahovat objekty různých velikostí nebo opakovaně jeden opakovatelný objekt pevné dimenze.
matematický model bude záviset na formě každé z těchto proměnných.
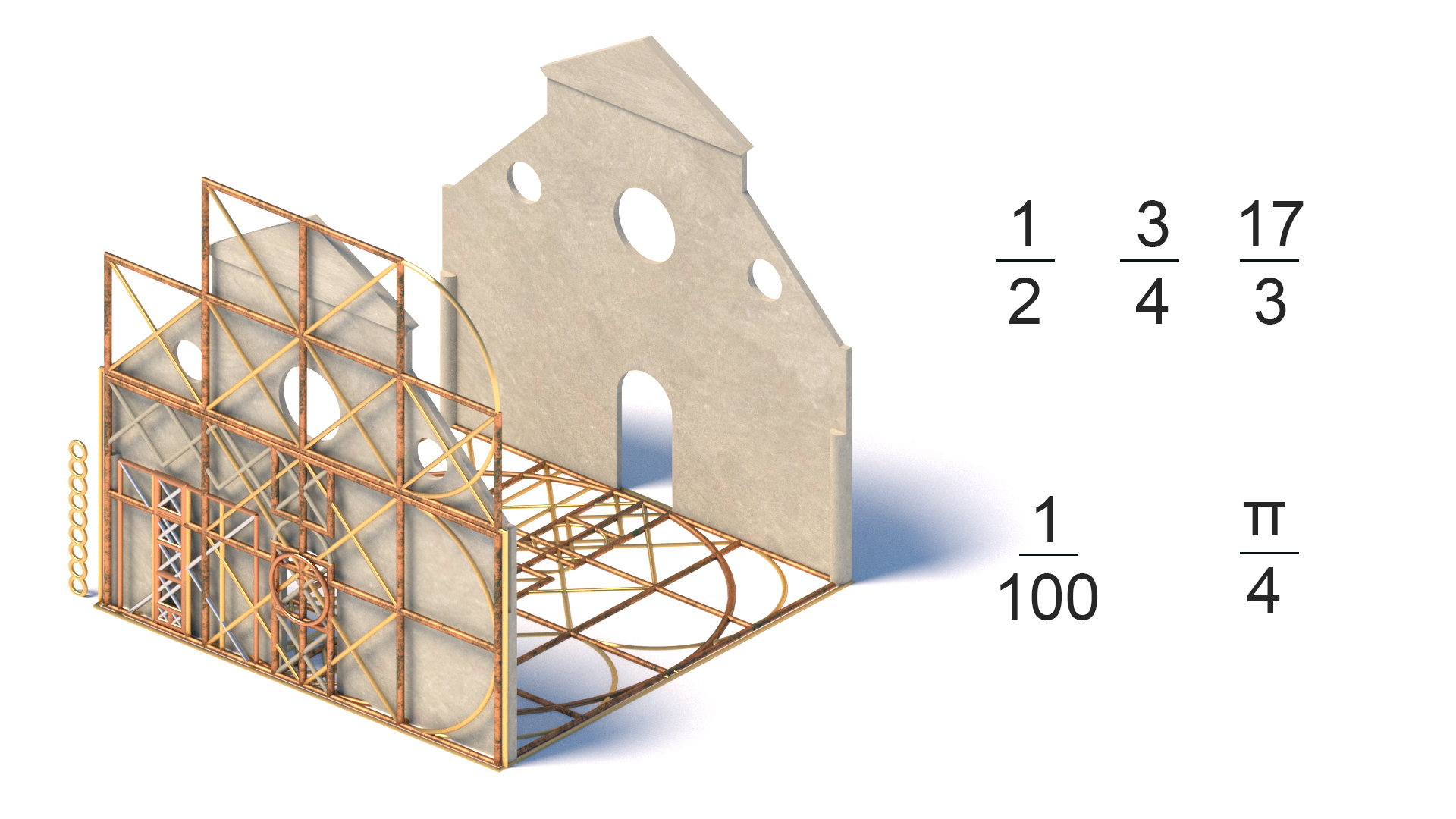
frakce
běžné použití před desetinnou čárkou (vynalezeno v 15. století). Budovy a umění byly dimenzovány z hlediska zlomků, buď násobení modulu, nebo rozdělení celku. Některé z nich by zahrnovaly dvě nebo více sad základní frakce ve stejné práci. Toto je jedna ze základních metod v klasické architektuře hledání ideální geometrie, která by mohla být frakčně rozdělena.
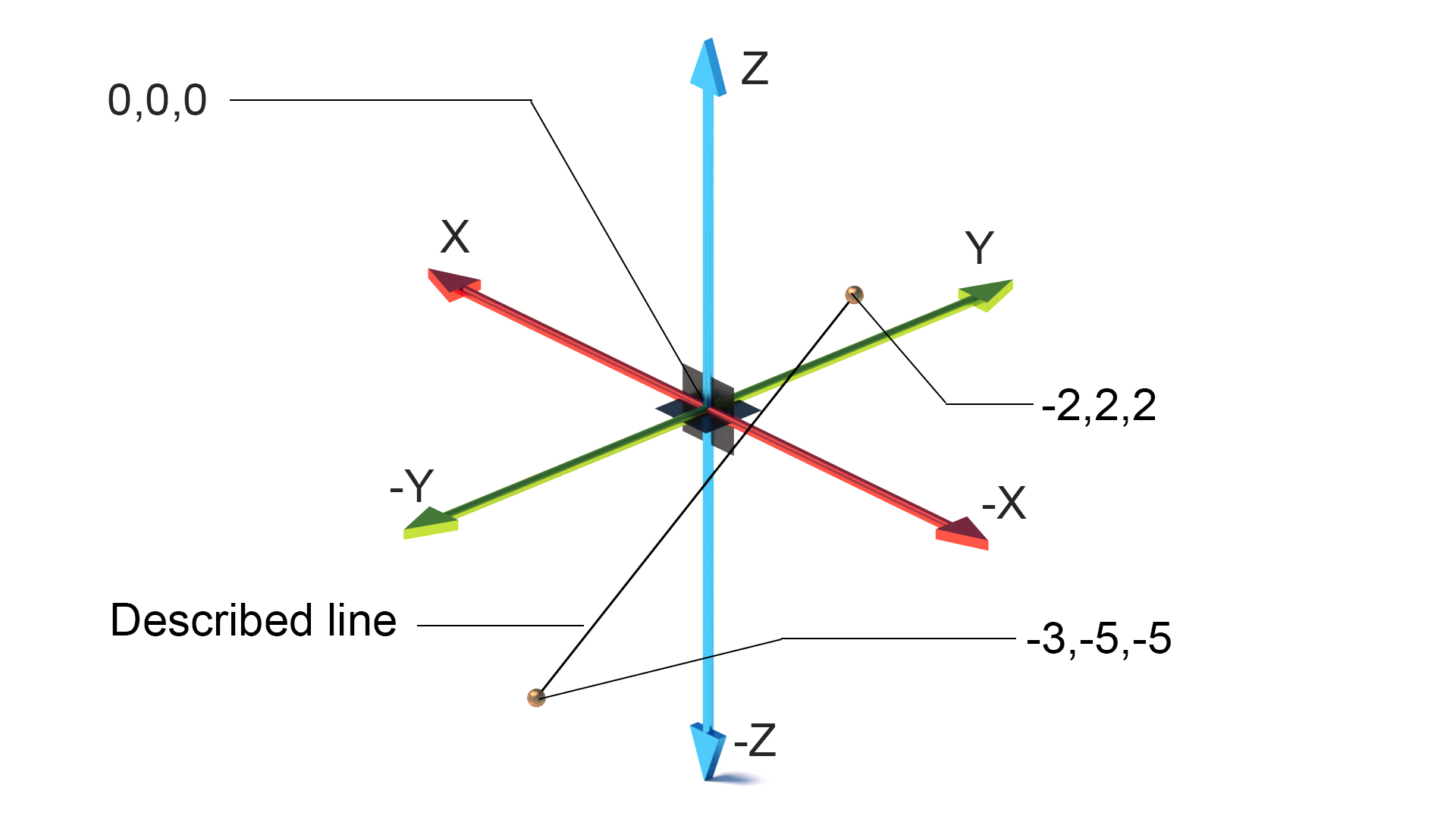
Kartézský souřadnicový systém
vynalezený v 17. století René Descartes z „myslím, že proto jsem“ sláva. Descartes měl myšlenku přeměnit ploché a trojrozměrné formy na numerické informace, které by umožnily přesné popisy světa matematickými prostředky.
v rovině (ploché) je souřadnicový systém tvořen body a určuje každý bod jedinečně dvojicí číselných souřadnic, což jsou vzdálenosti k bodu od dvou pevných kolmých čar (x a y při použití počítače), tyto referenční čáry se nazývají souřadnicová osa systému. Bod, kde se osy setkávají / kříží, je počáteční rovina 0,0.
v trojrozměrném prostoru se přidá třetí osa (Z), která udává výšku v systému. Všechny řádky se setkávají ve stejné rovině původu 0,0,0.
vektory lze také použít k popisu umístění bodu v úhlu a vzdálenosti od plánu původu nebo jiného bodu.
tento koordinační systém tvoří základ počítačového návrhového softwaru a je postaven na popisu složitějších geometrií.