den gennemsnitlige forretning har ændret sig radikalt i løbet af det sidste årti.

uanset om det er det udstyr, der bruges på skriveborde eller det program, der bruges til at kommunikere, ser meget få ting ud som de engang var.

noget andet, der er helt anderledes, er, hvor meget data vi har lige ved hånden. Det, der engang var knappe, er nu en tilsyneladende overvældende mængde data. Men det er kun overvældende, hvis du ikke ved, hvordan du analyserer din virksomheds data for at finde sand og indsigtsfuld betydning.

så hvordan går du fra punkt A med en enorm mængde data til punkt B og er i stand til nøjagtigt at fortolke disse data? Det hele handler om at bruge de rigtige metoder til statistisk analyse, hvilket er, hvordan vi behandler og indsamler prøver af data for at afdække mønstre og tendenser.

til denne analyse er der fem at vælge imellem: middelværdi, standardafvigelse, regression, hypotesetest og bestemmelse af stikprøvestørrelse.

de 5 metoder til udførelse af statistisk analyse

der kan ikke benægtes, at verden bliver besat af big data, uanset om du er dataforsker eller ej. På grund af dette skal du vide, hvor du skal starte. Disse fem metoder er grundlæggende, men alligevel effektive, når de kommer til nøjagtige datadrevne konklusioner.

middel

den første metode, der bruges til at udføre den statistiske analyse, er middel, som mere almindeligt kaldes gennemsnittet. Når du ønsker at beregne gennemsnittet, tilføjer du en liste med tal og deler derefter dette tal med elementerne på listen.

når denne metode anvendes, giver den mulighed for at bestemme den samlede tendens for et datasæt samt evnen til at opnå en hurtig og kortfattet visning af dataene. Brugere af denne metode drager også fordel af den forenklede og hurtige beregning.

det statistiske gennemsnit kommer op med det centrale punkt i de data, der behandles. Resultatet kaldes gennemsnittet af de leverede data. I det virkelige liv, folk bruger typisk middel til med hensyn til forskning, akademikere, og sport. Tænk på, hvor mange gange en spillers batting gennemsnit diskuteres i baseball; det er deres middelværdi.

Sådan finder du gennemsnittet

for at finde gennemsnittet af dine data skal du først tilføje tallene sammen og derefter dele summen med, hvor mange tal der er inden for datasættet eller listen.

som et eksempel, for at finde gennemsnittet af 6, 18 og 24, vil du først tilføje dem sammen.
6 + 18 + 24 = 48
derefter divideres med hvor mange tal i listen (3).
48 / 3 = 16
gennemsnittet er 16.

ulempen

når du bruger middelværdien er stor, anbefales det ikke som en selvstændig statistisk analysemetode. Dette skyldes, at dette potentielt kan ødelægge den komplette indsats bag beregningen, da det også er relateret til tilstanden (den værdi, der forekommer oftest) og median (midten) i nogle datasæt.

når du beskæftiger dig med et stort antal datapunkter med enten et stort antal outliers (et datapunkt, der adskiller sig væsentligt fra andre) eller en unøjagtig fordeling af data, giver middelværdien ikke de mest nøjagtige resultater i statistisk analyse til en bestemt beslutning.

standardafvigelse

standardafvigelse er en metode til statistisk analyse, der måler spredningen af data omkring gennemsnittet.

når du har at gøre med en høj standardafvigelse, peger dette på data, der er spredt bredt fra gennemsnittet. Tilsvarende viser en lav afvigelse, at de fleste data er i tråd med gennemsnittet og også kan kaldes den forventede værdi af et sæt.

standardafvigelse bruges hovedsageligt, når du har brug for at bestemme spredningen af datapunkter (uanset om de er grupperet eller ej).

lad os sige, at du er en marketingmedarbejder, der for nylig gennemførte en kundeundersøgelse. Når du får resultaterne af undersøgelsen, er du interesseret i at måle pålideligheden af svarene for at forudsige, om en større gruppe af kunder kan have de samme svar. Hvis der opstår en lav standardafvigelse, vil det vise, at svarene kan projiceres til en større gruppe kunder.

Sådan finder du standardafvigelsen

formlen til beregning af standardafvigelsen er:

i denne formel:

• symbolet for standardafvigelse er lussang
• Lussang står for summen af dataene
• kus står for værdien af datasættet
• lussang står for middelværdien af dataene
• lussang står for variansen
• n står for antallet af datapunkter i befolkningen

for at finde standardafvigelsen:

1. Find gennemsnittet af tallene i datasættet
2. for hvert tal i datasættet trækker du middelværdien og kvadrerer resultatet (som er denne del af formlen 2).
3. Find gennemsnittet af disse kvadrerede forskelle
4. Tag kvadratroden af det endelige svar

hvis du brugte de samme tre tal i vores gennemsnitlige eksempel, 6, 18 og 24, ville standardafvigelsen eller kur være 7.4833147735479.

ulempen

på en lignende note til ulempen ved at bruge middelværdi kan standardafvigelsen være vildledende, når den bruges som den eneste metode i din statistiske analyse.

som et eksempel, hvis de data, du arbejder med, har for mange outliers eller et mærkeligt mønster som en ikke-normal kurve, giver standardafvigelsen ikke de nødvendige oplysninger til at træffe en informeret beslutning.

Regression

når det kommer til statistik, er regression forholdet mellem en afhængig variabel (de data, du ønsker at måle) og en uafhængig variabel (de data, der bruges til at forudsige den afhængige variabel).

det kan også forklares ved, hvordan en variabel påvirker en anden, eller ændringer i en variabel, der udløser ændringer i en anden, i det væsentlige årsag og virkning. Det indebærer, at resultatet er afhængig af en eller flere variabler.

linjen, der bruges i regressionsanalysegrafer og diagrammer, betyder, om forholdet mellem variablerne er stærke eller svage, ud over at vise tendenser over en bestemt tidsperiode.

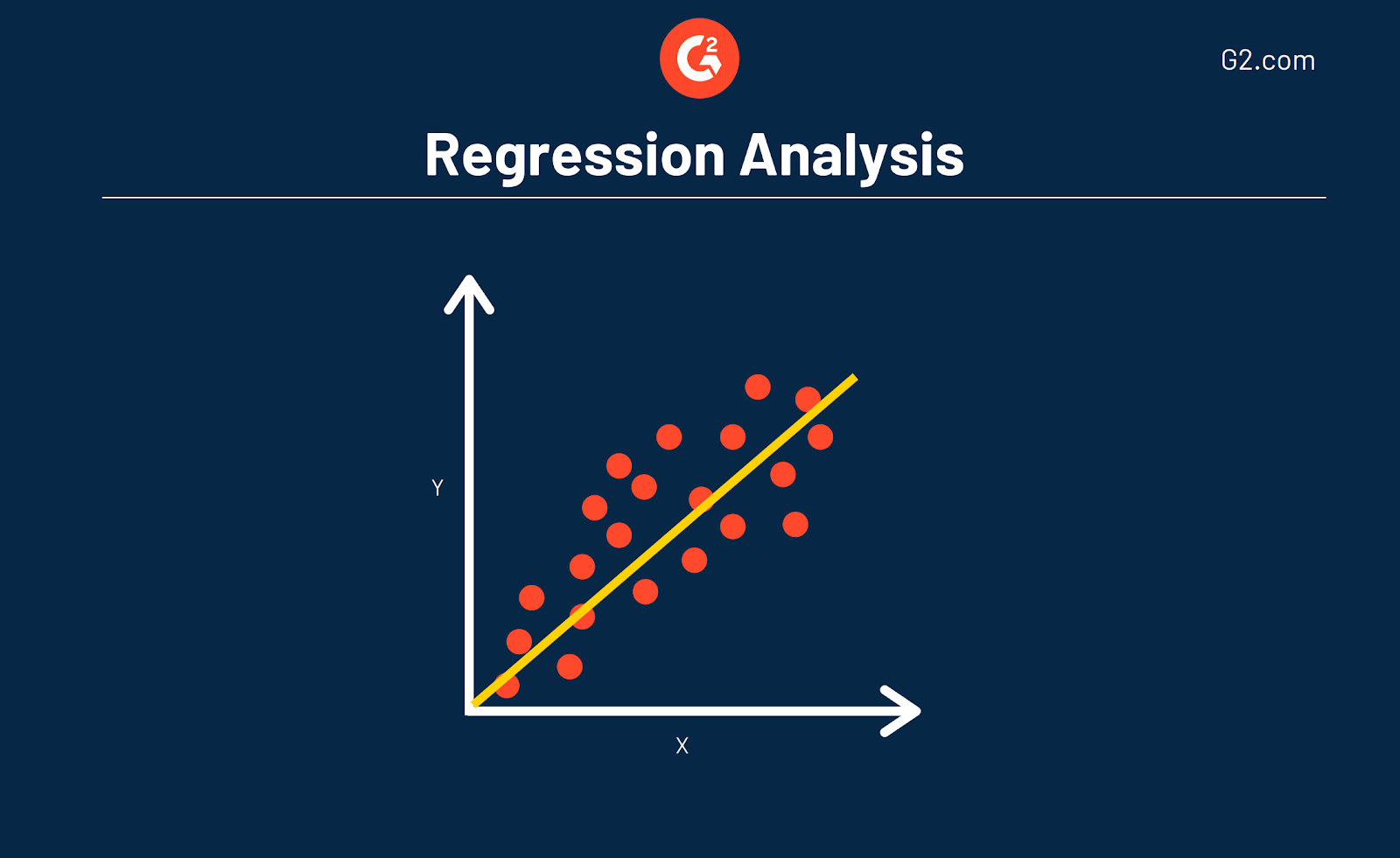
disse undersøgelser bruges i statistisk analyse til at forudsige og forudsige tendenser. Du kan f.eks. bruge regression til at forudsige, hvordan et bestemt produkt eller en bestemt tjeneste kan sælge til dine kunder. Eller her på G2 bruger vi regression til at forudsige, hvordan vores organiske trafik vil se ud 6 måneder fra nu.

Regressionsformel

regressionsformlen, der bruges til at se, hvordan data kunne se ud i fremtiden, er:

i denne formel:

• a henviser til Y-skæringspunktet, værdien af y når = 0
• er den afhængige variabel
• Y er den uafhængige variabel
• B henviser til hældningen eller stigningen over Løbet

ulempen

en ulempe ved brug af regression som en del af din statistiske analyse er, at regression ikke er meget karakteristisk, hvilket betyder, at selvom outliers på et scatter plot (eller regressionsanalysegraf) er vigtige, så er årsagerne til, hvorfor de er outliers. Denne årsag kan være alt fra en fejl i analysen til, at data bliver uhensigtsmæssigt skaleret.

et datapunkt, der er markeret som en outlier, kan repræsentere mange ting, såsom dit bedst sælgende produkt. Regressionslinjen lokker dig til at ignorere disse outliers og kun se tendenser i data.

hypotesetest

i statistisk analyse er hypotesetest, også kendt som “T-Test”, En nøgle til at teste de to sæt tilfældige variabler i datasættet.

denne metode handler om at teste, om et bestemt argument eller en konklusion er sandt for datasættet. Det giver mulighed for at sammenligne dataene med forskellige hypoteser og antagelser. Det kan også hjælpe med at forudsige, hvordan beslutninger, der træffes, kan påvirke virksomheden.

i statistik bestemmer en hypotesetest en vis mængde under en given antagelse. Resultatet af testen fortolker, om antagelsen holder, eller om antagelsen er blevet overtrådt. Denne antagelse kaldes nulhypotesen eller hypotese 0. Enhver anden hypotese, der ville være i strid med hypotese 0 kaldes den første hypotese, eller hypotese 1.

når du udfører hypotesetest, er resultaterne af testen vigtige for statistikken, hvis resultaterne er et bevis på, at det ikke kunne være sket ved en tilfældig forekomst eller chance.

som et eksempel kan du antage, at jo længere tid det tager at udvikle et produkt, jo mere vellykket vil det være, hvilket resulterer i højere salg end nogensinde før. Inden der implementeres længere arbejdstid for at udvikle et produkt, sikrer hypotesetestning, at der er en faktisk forbindelse mellem de to.

Hypotesetestformel

resultaterne af en statistisk hypotesetest skal fortolkes for at fremsætte et specifikt krav, der kaldes p-værdien.

lad os sige, at det, du ønsker at bestemme, har en 50% chance for at være korrekt.

formlen for denne hypotesetest er:

ulempen

hypotesetestning kan undertiden være overskyet og skævt af almindelige fejl, som placebo-effekten. Dette sker, når statistiske analytikere, der udfører testen, fejlagtigt forventer et bestemt resultat og derefter ser det resultat, uanset omstændighederne.

der er også sandsynligheden for at blive skæv af Hagtorne-effekten, ellers kendt som observatøreffekten. Dette sker, når deltagerne bliver analyseret skæv resultaterne, fordi de ved, at de bliver undersøgt.

bestemmelse af prøvestørrelse

når det kommer til analyse af data til statistisk analyse, er datasættet undertiden simpelthen for stort, hvilket gør det vanskeligt at indsamle nøjagtige data for hvert element i datasættet. Når dette er tilfældet, går de fleste ruten for at analysere en stikprøvestørrelse eller mindre størrelse af data, som kaldes bestemmelse af stikprøvestørrelse.

for at gøre dette korrekt skal du bestemme den rigtige størrelse af prøven for at være nøjagtig. Hvis prøvestørrelsen er for lille, har du ikke gyldige resultater i slutningen af din analyse.

for at komme til denne konklusion bruger du en af de mange data sampling metoder. Du kan gøre dette ved at sende en undersøgelse til dine kunder og derefter bruge den enkle stikprøvemetode til at vælge de kundedata, der skal analyseres tilfældigt.

på den anden side kan en stikprøvestørrelse, der er for stor, resultere i spildt tid og penge. For at bestemme stikprøvestørrelsen kan du undersøge aspekter som omkostninger, tid eller bekvemmeligheden ved at indsamle data.

Find en stikprøvestørrelse

i modsætning til de andre fire statistiske analysemetoder er der ikke en hård og hurtig formel, der skal bruges til at finde stikprøvestørrelsen.

der er dog nogle generelle tip, du skal huske på, når du bestemmer en stikprøvestørrelse:

1. når du overvejer en mindre stikprøvestørrelse, skal du foretage en folketælling
2. brug en stikprøvestørrelse fra en undersøgelse, der ligner din egen. Til dette kan du overveje at kigge på akademiske databaser for at søge efter en lignende undersøgelse
3. hvis du gennemfører en generisk undersøgelse, kan der være en tabel, der allerede findes, som du kan bruge til din fordel
4. brug en prøvestørrelsesberegner
5. bare fordi der ikke er en bestemt formel, betyder det ikke, at du ikke kan finde en formel, der fungerer. Der er mange, du kan bruge, og det afhænger af, hvad du ved eller ikke ved om den tilsigtede prøve. Nogle, som du måske overvejer at bruge, er Slovins formel og Cochrans formel

ulempen

når du analyserer en ny og uprøvet variabel af data inden for denne metode, skal du stole på visse antagelser. Dette kan resultere i en fuldstændig unøjagtig antagelse. Hvis denne fejl opstår under denne statistiske analysemetode, kan den påvirke resten af din dataanalyse negativt.

disse fejl kaldes prøveudtagningsfejl og måles med et konfidensinterval. For eksempel, hvis du angiver, at dine resultater er på et 90% konfidensniveau, betyder det, at hvis du skulle udføre den samme analyse igen og igen, vil 90% af tiden dine resultater være de samme.

en metode til galskaben

uanset hvilken metode til statistisk analyse du vælger, skal du sørge for at være særlig opmærksom på hver potentiel ulempe såvel som deres unikke formel.

selvfølgelig er der ingen guldstandard eller rigtig eller forkert metode at bruge. Det vil afhænge af den type data, du har indsamlet, samt den indsigt, du ønsker at have som et slutresultat.

interesseret i at finde det rigtige værktøj til at tage dit kig på data endnu længere? Se vores oversigt over de bedste statistiske analyseprogrammer til selv de mest komplekse analyser.