klassisk matematik er tæt knyttet til klassisk geometri i arkitektur. Et emne, Jeg har diskuteret i et tidligere indlæg her. Dette er ikke en komplet liste over metoder eller formler, men et simpelt overblik over de metoder, arkitekter tidligere har brugt. Med henblik på forenkling udelukker vi strukturelle beregninger, der er baseret på materialer, skala og belastninger og derfor for brede til et simpelt blogindlæg.
traditionelt brugt af matematik
selvom vi ofte omtaler dette som tidligere, er der stadig en løbende tradition for klassisk arkitektur, både som folkesprog og klassicisme. Den traditionelle brug af matematik kan forenkles i 4 områder:
- strukturelle beregninger
- geometri og rumlige former
- Form æstetik eller tro på skønhed, der stammer fra former; proportioner og symmetrier.
- dekorationer af overflader og former i det rumlige miljø
modernismen flyttede væk fra dette på mange måder, men en voksende interesse for parametrisk arkitektur har genoplyst en interesse for matematik og geometri i arkitektur. Dette er blevet beriget i post-calculus æra med beregning af miljømæssige og funktionelle parametre. Et emne, der vil blive udforsket i et andet separat indlæg.
strukturel beregning er et væsentligt emne og vil ikke blive dækket detaljeret her. Tilstrækkeligt til at sige, at strukturelt design udviklede sig fra estimering af materialekvaliteter til en informeret beregning inden konstruktionen. Et område eller arkitektonisk teori” materielle kulturer ” teoretiserer, at en arkitektonisk kulturel vækst sker, når en traditionel konstruktionsmetode bevæger sig fra et materiale til et andet. Et eksempel er den klassiske vestlige arkitektur, der oprindeligt var træ, der derefter blev oversat til sten. Elementerne i klassisk arkitektur bærer stadig disse originale trædetaljer, der nu bruges som rene dekorationer i sten. Omfanget og teknologien for de nye materialekomponenter ville naturligvis skulle ændres i oversættelsen og skabe en ny æstetik.
geometri
mens geometrien og rumlige former er afledt af matematik, diskuterede jeg dette i et separat indlæg.
guderne eller naturen
natur og religion har altid været grundlæggende i designet af vores miljø. Tidlige agrariske kulturer ville identificere, at naturen fulgte regler, der kunne oversættes til matematik, fra proportionale regler til fraktalisering for at nævne to. Dette blev taget som et bevis for, at universet blev designet af guderne. Så naturligvis skulle tilbedelsesstederne bruge disse” hellige ” regler. Disse regler ville derefter diffundere ind i andre magtsteder og derefter ind i den generelle folkelige brug.
den religiøse brug af disse matematik har tendens til at ligge til grund for et symbolsk udtryk for gudfrygtig design, mens sekulær brug har været mere repræsentativ for naturen. Brugen af disse matematik og geometrier har derfor svinget mellem disse metoder afhængigt af datidens filosofi med tild af overlapning.

Golden Section/Ratio
to mængder med en ration til hinanden, der er den samme som rationen af deres sum til den største af mængderne. Den gyldne sektion blev betragtet som en kerne æstetisk form på grund af dens rigelige eksempel i naturen. Æstetisk teori hævder, at det er særlig skønhed stammer fra, at formen er en “imellem” mellem en firkant og et rektangel.
fra klassiske græske templer til Renæssancekirker og Corbusier-facader er dette uden tvivl den mest genkendelige klassiske formel i både samlet geometri og bygningsdetaljer.
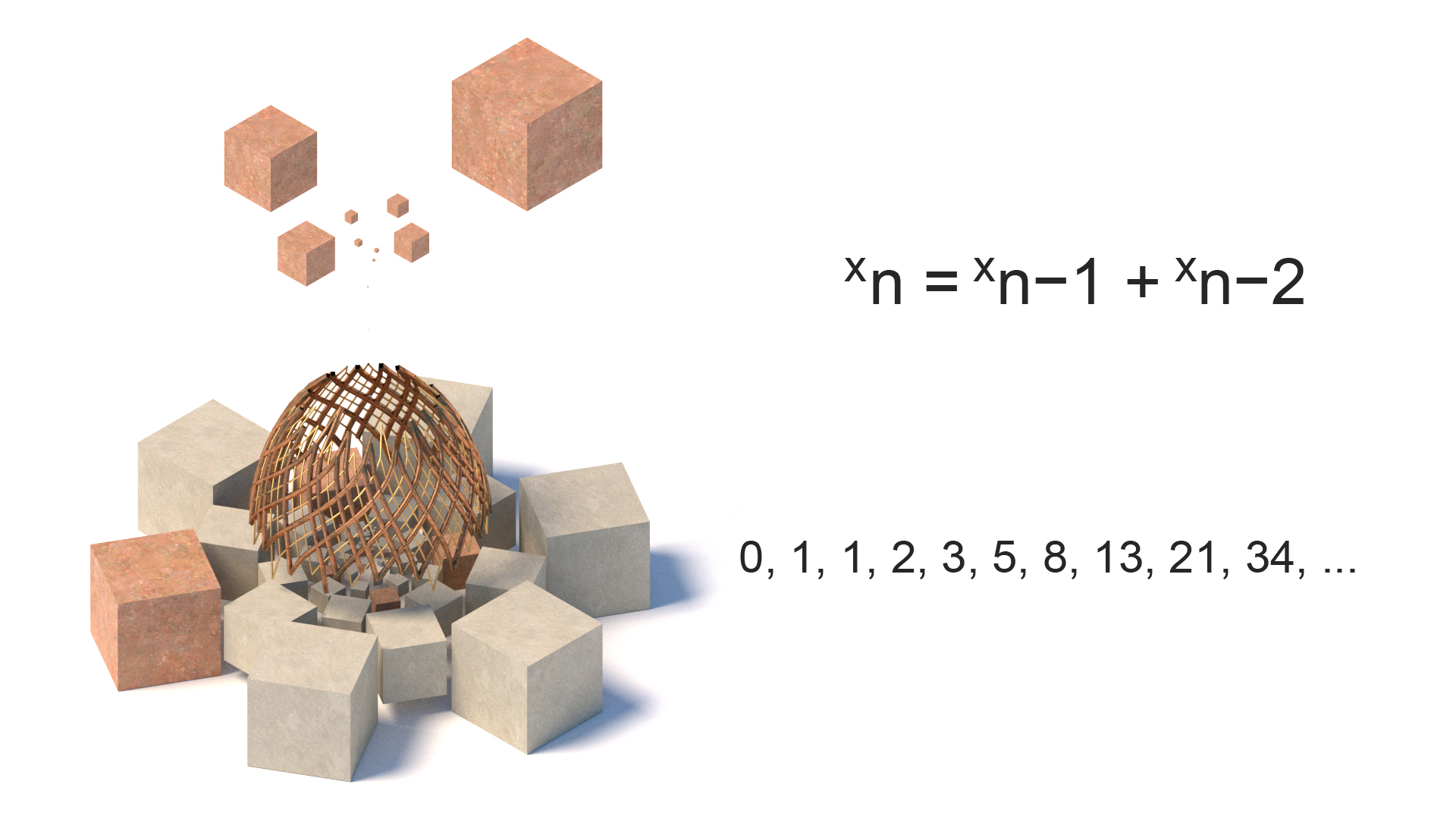
Fibonacci-numre
Fibonacci-sekvensen er opkaldt efter den italienske matematiker Leonardo fra Pisa, hvor hvert tal er summen af de to procedurenumre. Sekvensen, hvis observeret hyppigt i naturen, såsom i træ forgrening, kogler osv. Brugen af dette i spiralformer kan findes i alt fra klassiske græske templer til Mona Lisa.
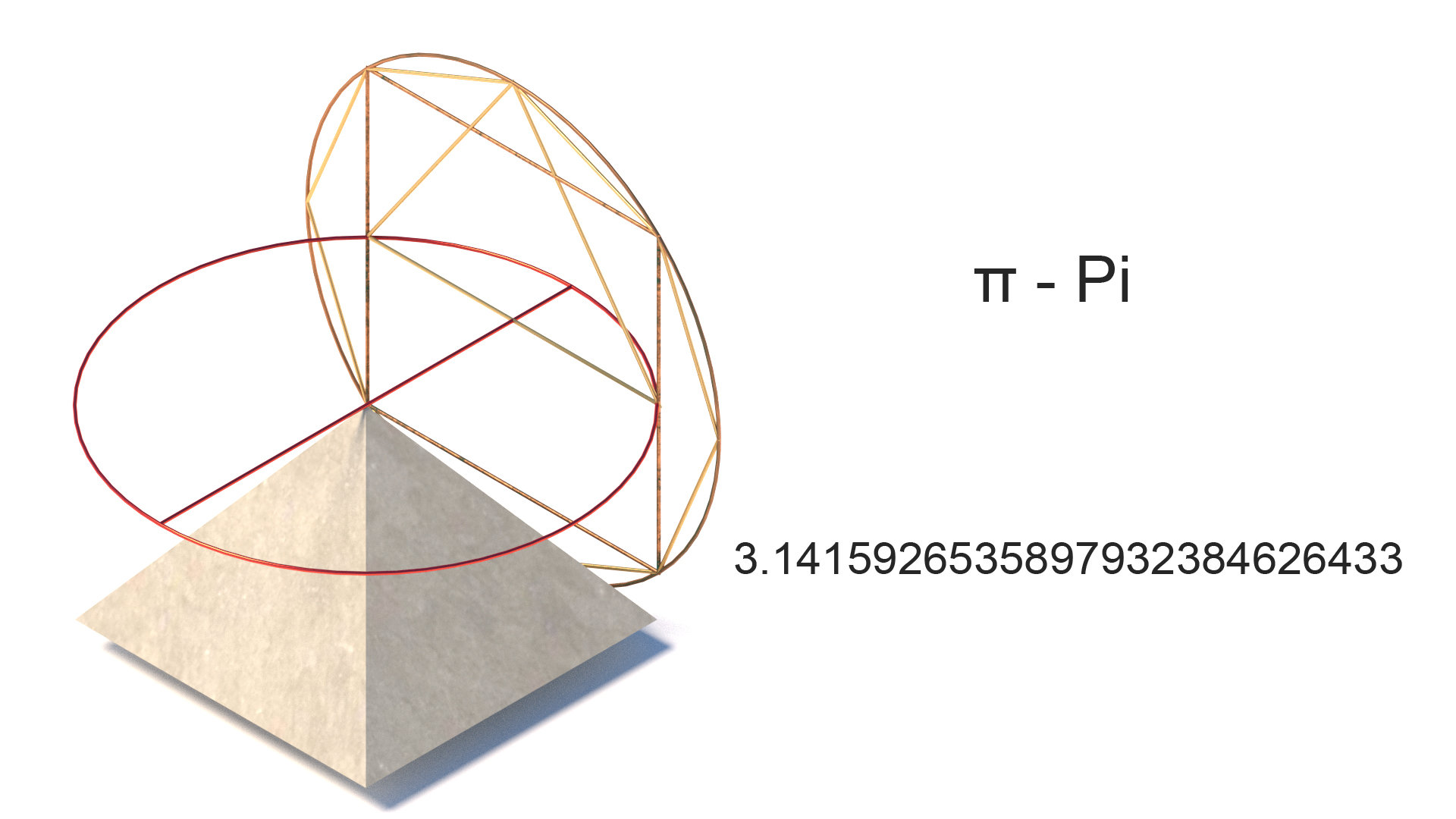
Pi liter
Pi er grundlæggende forholdet mellem en cirkels omkreds og dens diameter og svarer til cirka 3.14159. Repræsenteret af den græske” Kristian ” siden det 18.århundrede. Mens pi er nyttigt til at” kvadrere en cirkel ” og beregne brugen af cirkulære former, er der fundet andre anvendelser fra fortiden. John Taylor (1859) opdagede, at hvis pyramidens omkreds er divideret med dens højde, er resultatet en tæt tilnærmelse til 2 &pi.
Pi kan hjælpe med at måle ting som væske, lyd og lysbølger og sandsynlighed som fordelingen af noder i moderne beregningsbaseret matematik. Det er derfor kernen i mange moderne parametriske beregninger.
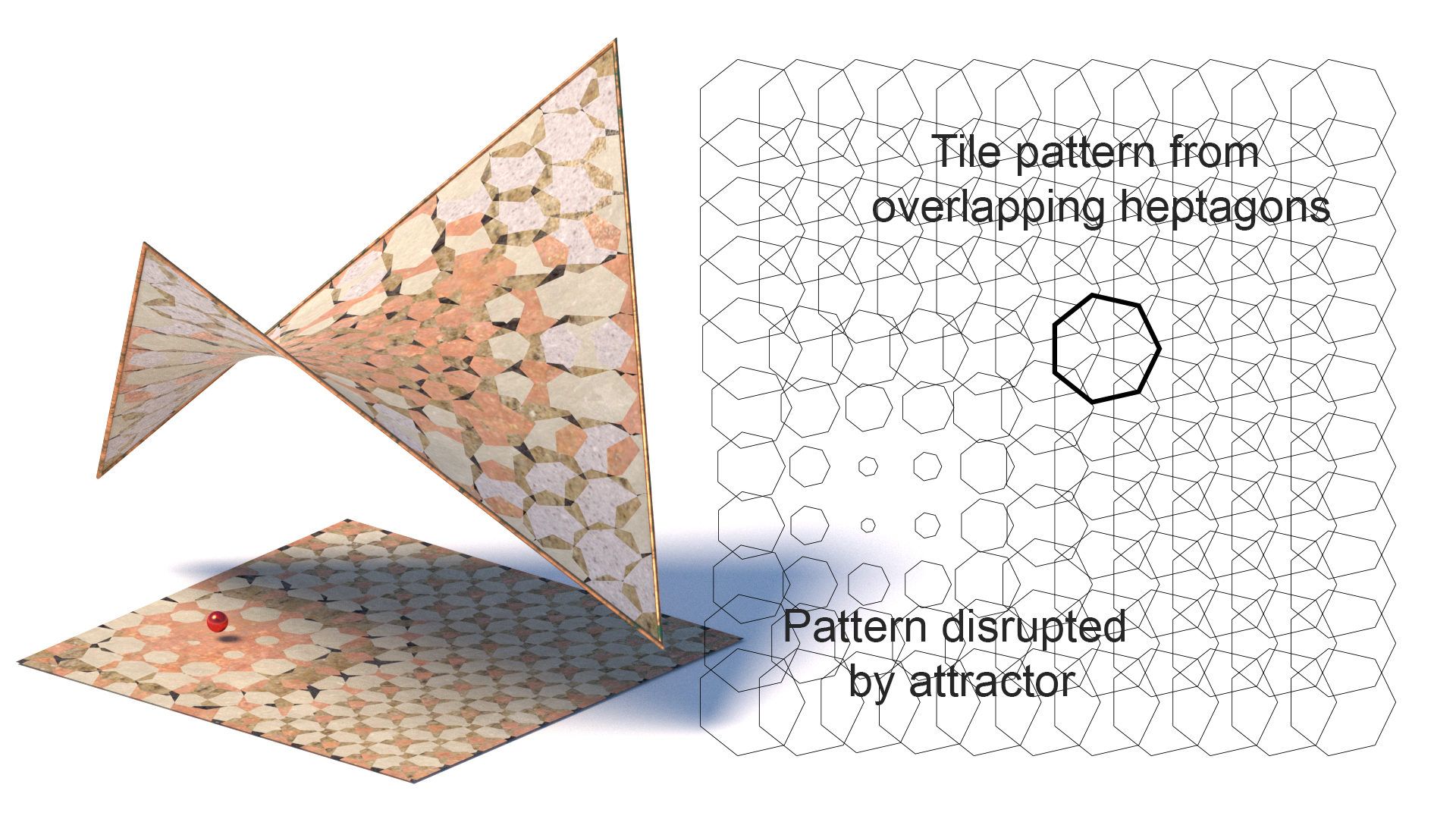
2D og 3D flisebelægning
Tessellation (flisebelægning)
flisebelægning involveret dækker en plan overflade i geometriske former. Den enkleste omfatter rektangulære fliser som ofte bruges i badeværelser og køkkener. Mere komplicerede former kræver en mere komplekse metoder til gentagne geometrier. Den klassiske matematik af gentagne mønstre var højt udviklet i Mellemøsten og Sydøstasien. Der er mange forskellige former for tesselationer, nogle populære inkluderer:
- regelmæssig tessellation er en kant til kant symmetrisk flisebelægning.
- Semi-regular / Archimedean tessellation bruger mere end en type regelmæssig polygon i et isogonalt arrangement
- Monohedral flisebelægning er en tessellation, hvor alle fliser har samme form og størrelse.
- Isohedral flisebelægning er en speciel variation af en monohedral flisebelægning, hvor alle fliser hører til den samme transitivitetsklasse
- Voronoi /Dirichlet flisebelægninger er tessellationer, hvor hver flise er defineret som det sæt punkter, der er tættest på et af punkterne i et diskret sæt definerende punkter.
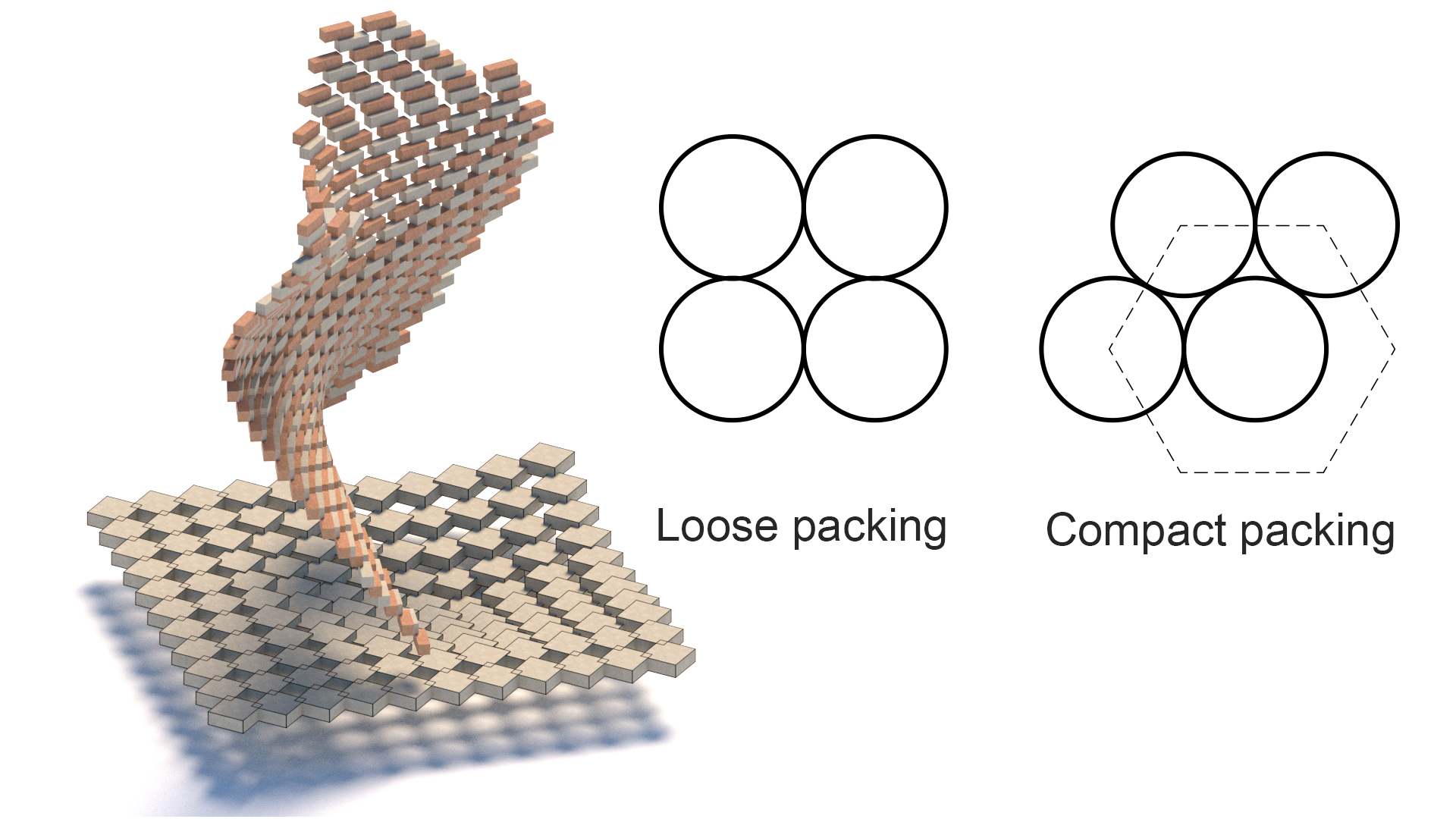
klassisk arkitektur pakning
pakning
en version af tessellation, pakning involverer stabling og sammenføjning af 3 dimensionelle enheder i et sammenhængende mønster med et varieret niveau af tæthed.
et pakningsproblem indeholder to variabler:
- en ‘containere’; normalt en enkelt to-eller tredimensionel region eller et uendeligt rum
- et sæt ‘objekter’, der skal pakkes i en eller flere containere. Sættet kan indeholde objekter i forskellige størrelser eller et enkelt gentageligt objekt med en fast dimension gentagne gange.
den matematiske model afhænger af formen for hver af disse variabler.
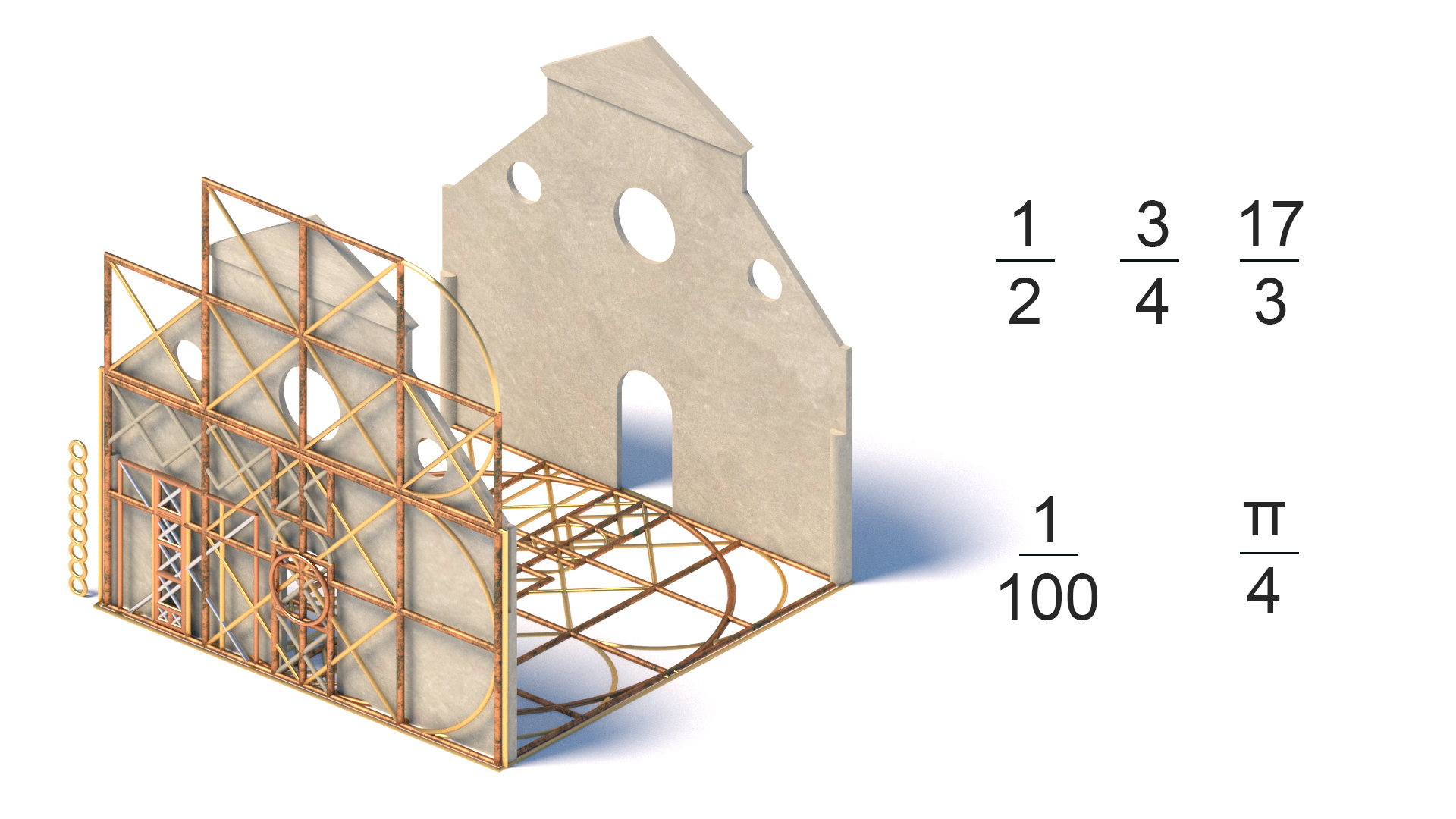
fraktioner
en almindelig brug før decimaltegn (opfundet i det 15.århundrede). Bygninger og kunst blev dimensioneret i form af fraktioner, enten multiplikation af et modul eller opdeling af helheden. Somethimes disse vil omfatte to eller flere sæt basisfraktion i det samme arbejde. Dette er en af kernemetoderne i den klassiske arkitektursøgning efter den ideelle geometri, der kunne opdeles fraktioneret.
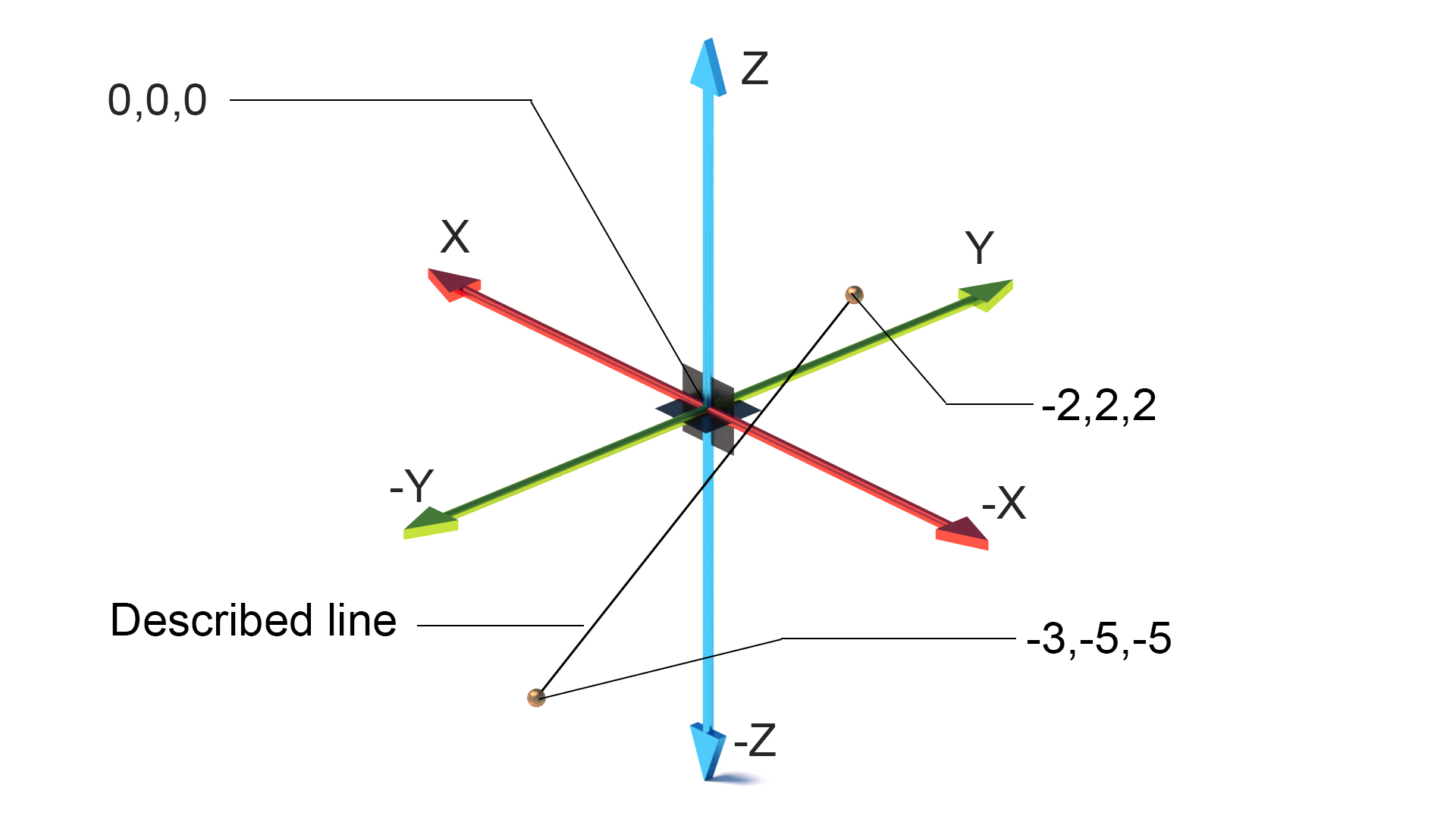
kartesisk koordinatsystem
opfundet i det 17.århundrede af ren Kristian Descartes af “Jeg tror derfor jeg er” berømmelse. Descartes havde ideen om at omdanne flade og tredimensionelle former til numerisk information, der ville give mulighed for nøjagtige beskrivelser af verden gennem matematiske midler.
i flyet (fladt) koordinatsystemet består af punkter og specificerer hvert punkt entydigt ved hjælp af et par numeriske koordinater, som er afstandene til punktet fra to faste vinkelrette linjer (h og y i computerbrug), disse referencelinjer kaldes en koordinatakse af systemet. Det punkt, hvor akserne mødes / krydses, er oprindelsesplanet 0,0.
i et 3-dimensionelt rum tilføjes en tredje akse (å) for at give højden i systemet. Alle linjer mødes på samme oprindelse plan 0,0,0.
vektorer kan også bruges til at beskrive placeringen af et punkt i en vinkel og afstand fra oprindelsesplanen eller et andet punkt.
dette koordineringssystem danner grundlaget for computerstøttet designprogram og er bygget på at beskrive mere komplekse geometrier.