Klassische Mathematik ist eng mit der klassischen Geometrie in der Architektur verwandt. Ein Thema, das ich in einem früheren Beitrag hier diskutiert habe. Dies ist keine vollständige Liste von Methoden oder Formeln, sondern eine einfache Übersicht über die Methoden, die Architekten in der Vergangenheit verwendet haben. Aus Gründen der Vereinfachung schließen wir Tragwerksberechnungen aus, die auf Materialien, Maßstab und Lasten basieren und daher für einen einfachen Blogbeitrag zu umfangreich sind.
Traditionell verwendet von Mathematik
Obwohl wir dies oft als Vergangenheit bezeichnen, gibt es immer noch eine anhaltende Tradition der klassischen Architektur, sowohl als Volkssprache als auch als Klassizismus. Die traditionelle Verwendung von Mathematik kann in 4 Bereiche vereinfacht werden:
- Strukturberechnungen
- Geometrie und Raumformen
- Formästhetik oder Glaube an Schönheit, die sich aus Formen ergibt; Proportionen und Symmetrien.
- Dekorationen von Oberflächen und Formen in der räumlichen Umgebung
Die Moderne entfernte sich in vielerlei Hinsicht davon, aber ein wachsendes Interesse an parametrischer Architektur hat ein Interesse an Mathematik und Geometrie in der Architektur wiederbelebt. Dies wurde in der Post-Kalkül-Ära mit der Berechnung von Umwelt- und Funktionsparametern angereichert. Ein Thema, das in einem anderen separaten Beitrag behandelt wird.
Die Tragwerksberechnung ist ein wesentliches Thema und wird hier nicht im Detail behandelt. Es genügt zu sagen, dass sich die Tragwerksplanung von der Schätzung der Materialqualitäten zu einer fundierten Berechnung vor dem Bau entwickelt hat. Ein Bereich oder Architekturtheorie „Materielle Kulturen“ theoretisiert, dass ein architektonisches kulturelles Wachstum stattfindet, wenn sich eine traditionelle Bauweise von einem Material zum anderen bewegt. Ein Beispiel ist die klassische westliche Architektur, die ursprünglich aus Holz bestand, das dann in Stein übersetzt wurde. Die Elemente der klassischen Architektur tragen immer noch diese ursprünglichen Holzdetails, die jetzt als reine Dekorationen in Stein verwendet werden. Der Maßstab und die Technologie der neuen Materialkomponenten müssten sich natürlich in der Übersetzung ändern, um eine neue Ästhetik zu schaffen.
Geometrie
Während die Geometrie und die räumlichen Formen aus der Mathematik abgeleitet sind, habe ich dies in einem separaten Beitrag besprochen.
Die Götter oder die Natur
Natur und Religion waren schon immer grundlegend für die Gestaltung unserer Umwelt. Frühe Agrarkulturen würden erkennen, dass die Natur Regeln folgte, die in Mathematik übersetzt werden konnten, von proportionalen Regeln bis zur Fraktalisierung, um zwei zu nennen. Dies wurde als Beweis dafür genommen, dass das Universum von den Göttern entworfen wurde. Natürlich müssten die Kultstätten diese „heiligen“ Regeln anwenden. Diese Regeln würden dann in andere Orte der Macht und dann in den allgemeinen Volksmund diffundieren.
Der religiöse Gebrauch dieser Mathematik lag tendenziell einem symbolischen Ausdruck göttlichen Entwurfs zugrunde, während der weltliche Gebrauch eher repräsentativ für die Natur war. Die Verwendung dieser Mathematik und Geometrien hat daher je nach Philosophie der Zeit zwischen diesen Methoden geschwungen, mit viel Überlappung.

Goldener Schnitt / Verhältnis
Zwei Größen mit einem Verhältnis zueinander, das dem Verhältnis ihrer Summe zur größeren der Größen entspricht. Der goldene Schnitt wurde aufgrund seines reichhaltigen Beispiels in der Natur als ästhetische Kernform angesehen. Die ästhetische Theorie behauptet, dass ihre besondere Schönheit von der Form herrührt, die ein „Dazwischen“ zwischen einem Quadrat und einem Rechteck ist.
Von klassischen griechischen Tempeln über Renaissancekirchen bis hin zu Corbusier-Fassaden ist dies wohl die bekannteste klassische Formel sowohl in der Gesamtgeometrie als auch in den Gebäudedetails.
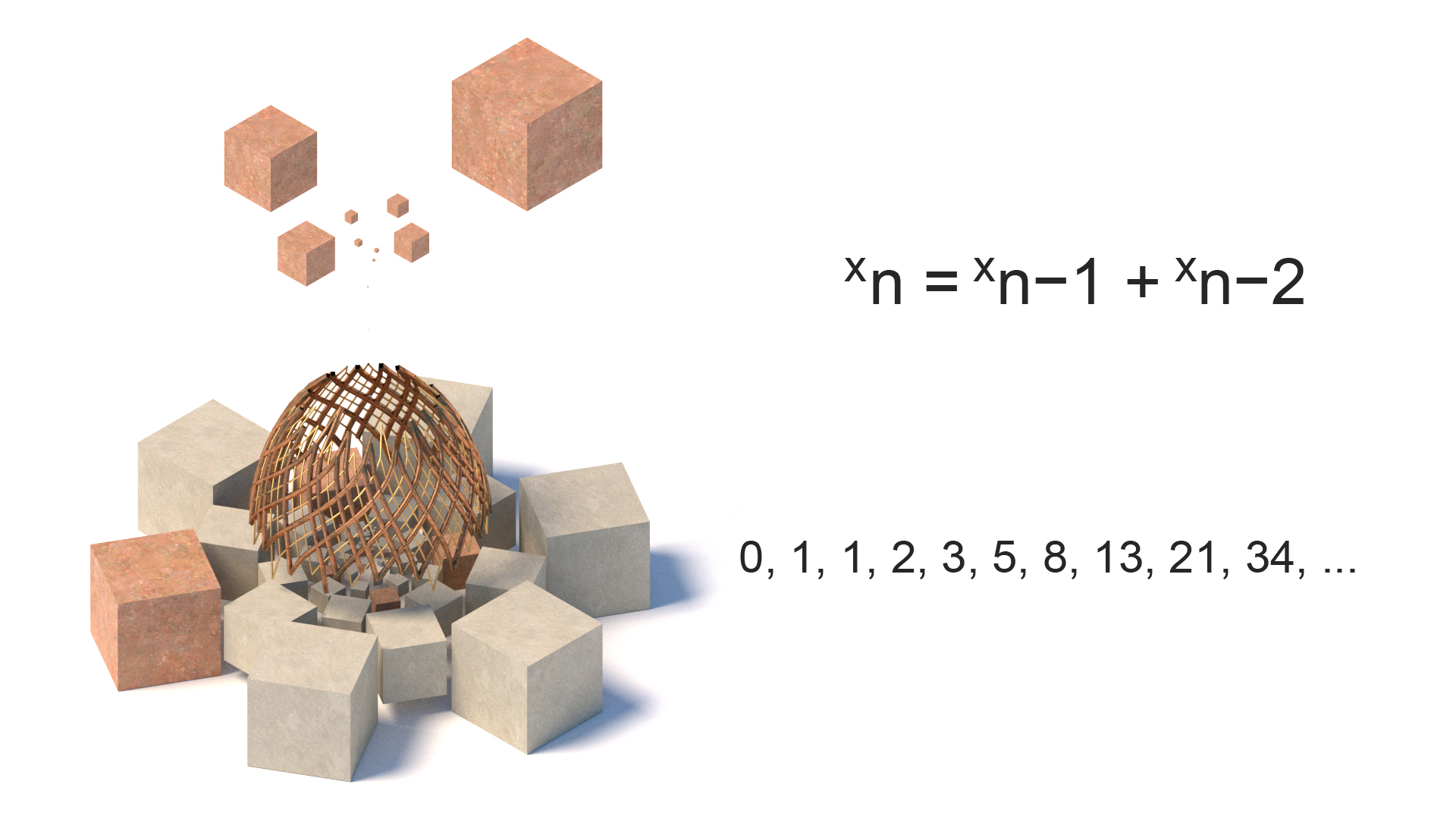
Fibonacci-Zahlen
Benannt nach dem italienischen Mathematiker Leonardo von Pisa, sind Fibonacci-Sequenzen Zahlen, bei denen jede Zahl die Summe der beiden vorangegangenen Zahlen ist. Die Sequenz wird häufig in der Natur beobachtet, z. B. bei Baumverzweigungen, Tannenzapfen usw. Die Verwendung in Spiralformen findet sich in allen Bereichen, von klassischen griechischen Tempeln bis zur Mona Lisa.
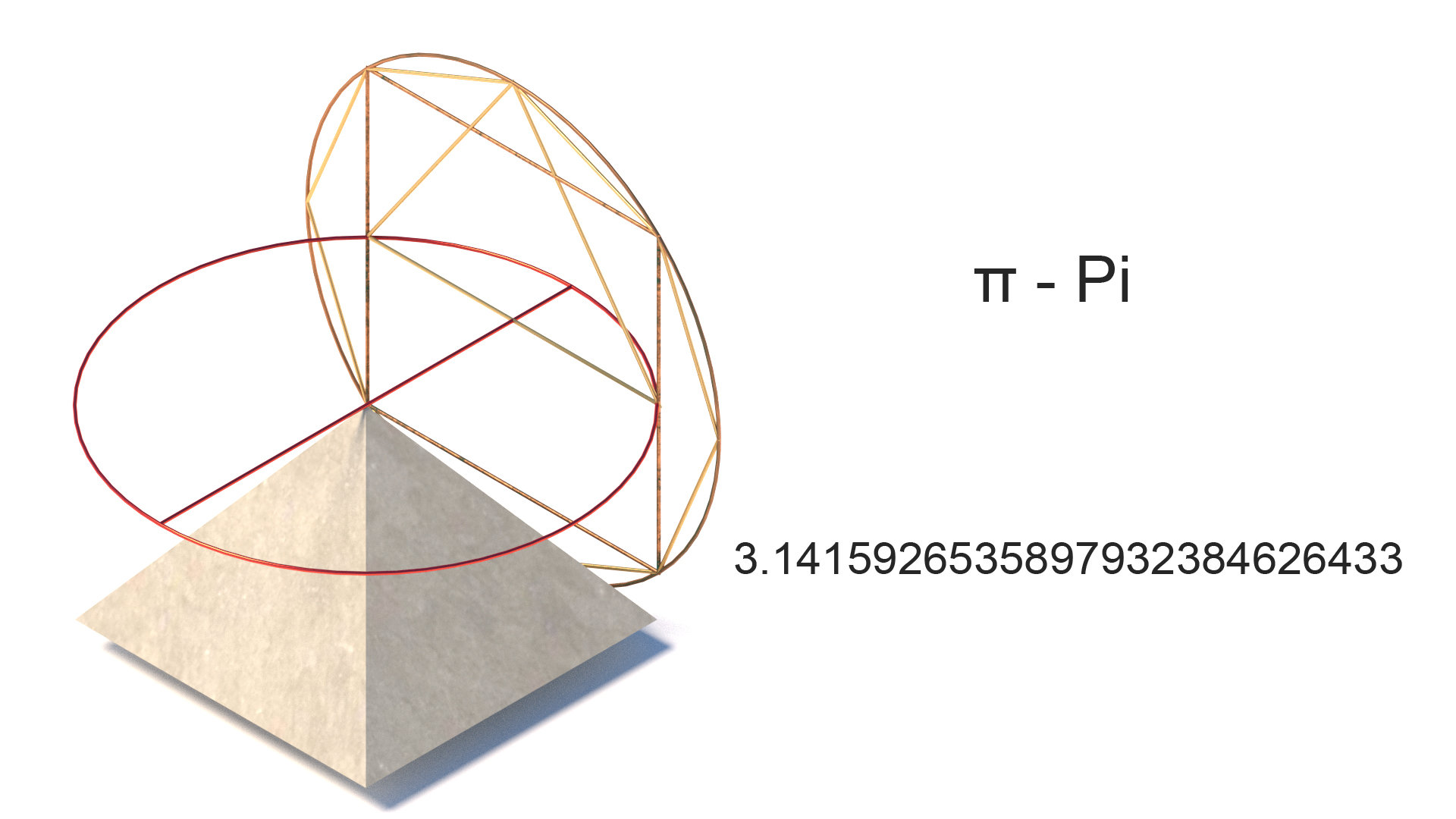
Pi π
Pi ist grundsätzlich das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser und entspricht ungefähr 3,14159. Vertreten durch das griechische „π“ seit dem 18. Während pi nützlich ist, um einen Kreis zu „quadrieren“ und die Verwendung von Kreisformen zu berechnen, wurden andere Verwendungen aus der Vergangenheit gefunden. John Taylor (1859) entdeckte, dass, wenn der Umfang der Pyramide durch ihre Höhe geteilt wird, das Ergebnis eine enge Annäherung an 2 & pi ist.
Pi kann helfen, Dinge wie Flüssigkeits-, Schall- und Lichtwellen und Wahrscheinlichkeiten wie die Verteilung von Knoten in der zeitgenössischen Kalkül-basierten Mathematik zu messen. Es ist daher der Kern vieler zeitgenössischer parametrischer Berechnungen.
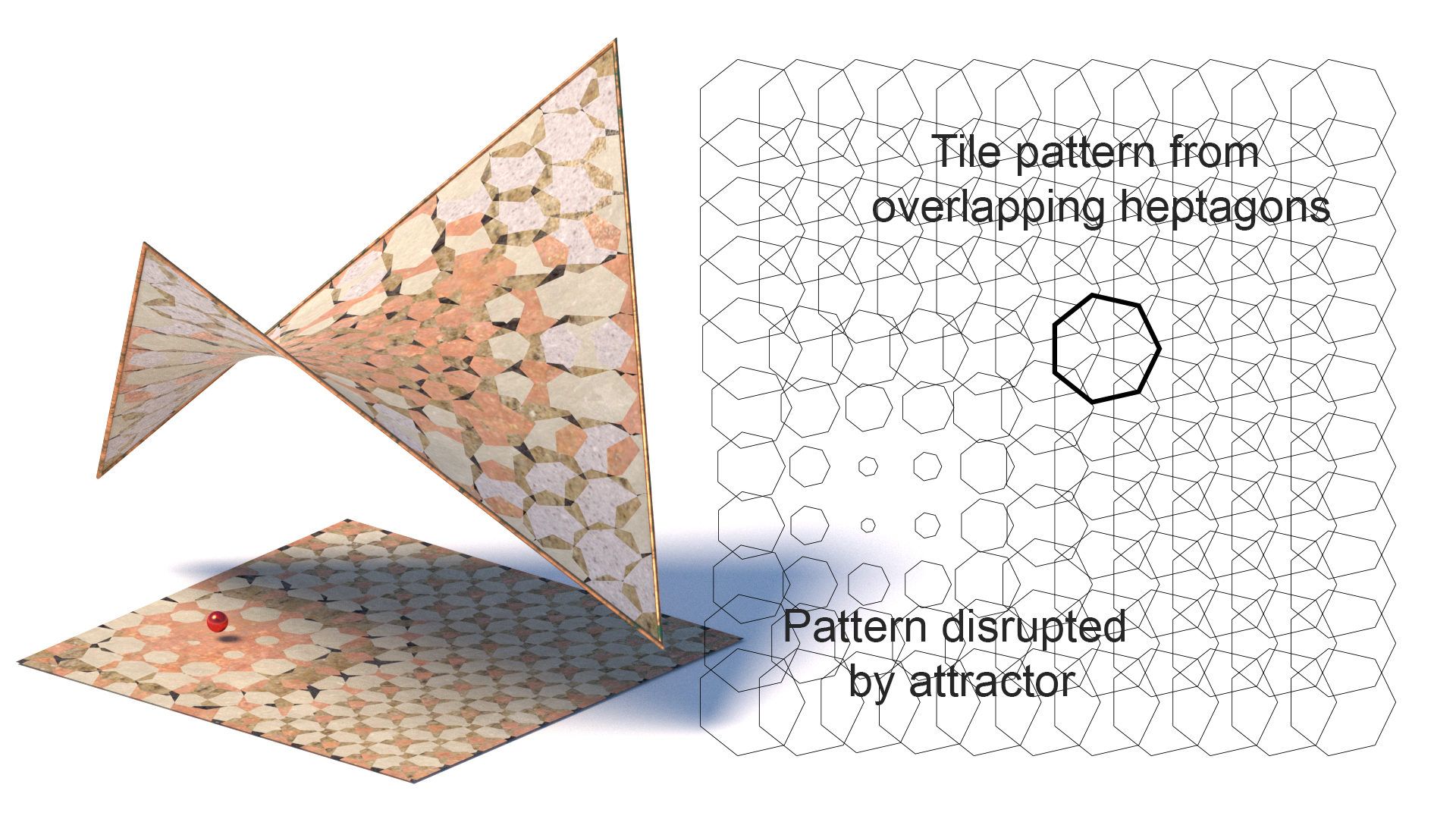
2D- und 3D-Fliesen
Tessellation (Fliesen)
Fliesen umfassten das Abdecken einer ebenen Oberfläche in geometrischen Formen. Zu den einfachsten gehören rechteckige Fliesen, wie sie häufig in Badezimmern und Küchen verwendet werden. Kompliziertere Formen erfordern komplexere Methoden für sich wiederholende Geometrien. Die klassische Mathematik der sich wiederholenden Muster war im Nahen Osten und in Südostasien hoch entwickelt. Es gibt viele verschiedene Formen von Mosaiken, einige beliebte sind:
- Regular Tessellation ist eine symmetrische Kachelung von Kante zu Kante.
- Semi-regular / Archimedische Tessellation verwendet mehr als eine Art von regelmäßigen Polygon in einer isogonalen Anordnung
- Monohedral Fliesen ist eine Tessellation, in der alle Fliesen die gleiche Form und Größe haben.
- Isohedral Tiling ist eine spezielle Variante einer Monohedral Tiling, bei der alle Kacheln derselben Transitivitätsklasse angehören
- Voronoi / Dirichlet-Kacheln sind Tessellationen, bei denen jede Kachel als die Menge von Punkten definiert ist, die einem der Punkte in einer diskreten Menge von definierenden Punkten am nächsten liegen.
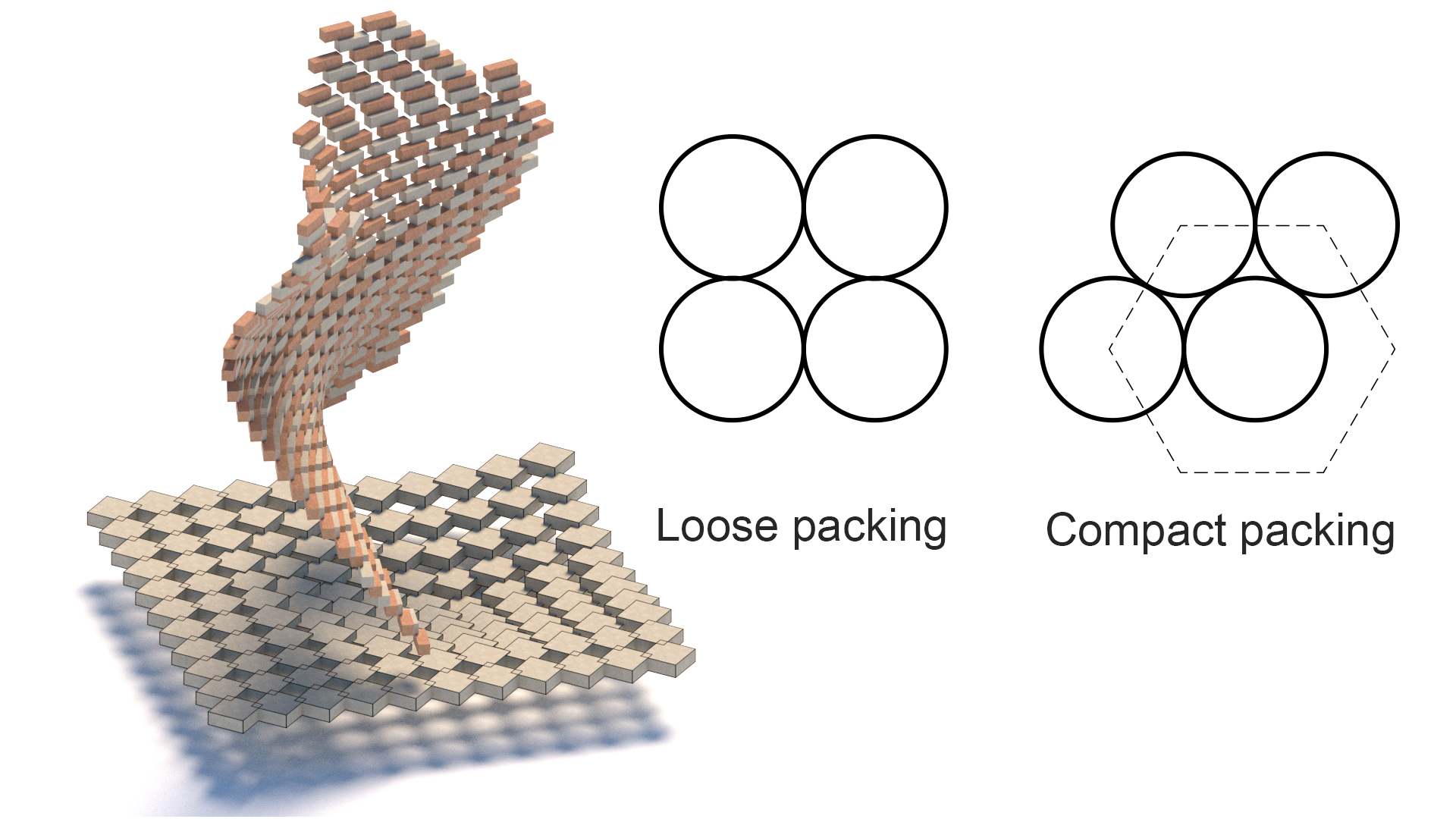
Klassische Architektur Verpackung
Verpackung
Bei einer Version der Tessellation handelt es sich bei der Verpackung um das Stapeln und Verbinden von 3-dimensionalen Einheiten zu einem kohärenten Muster mit unterschiedlichem Dichtegrad.
Ein Verpackungsproblem enthält zwei Variablen:
- Ein ‚Container‘; normalerweise ein einzelner zwei- oder dreidimensionaler Bereich oder ein unendlicher Raum
- Ein Satz von ‚Objekten‘, die in einen oder mehrere Container gepackt werden sollen. Der Satz kann Objekte unterschiedlicher Größe oder ein einzelnes wiederholbares Objekt einer festen Dimension wiederholt enthalten.
Das mathematische Modell hängt von der Form jeder dieser Variablen ab.
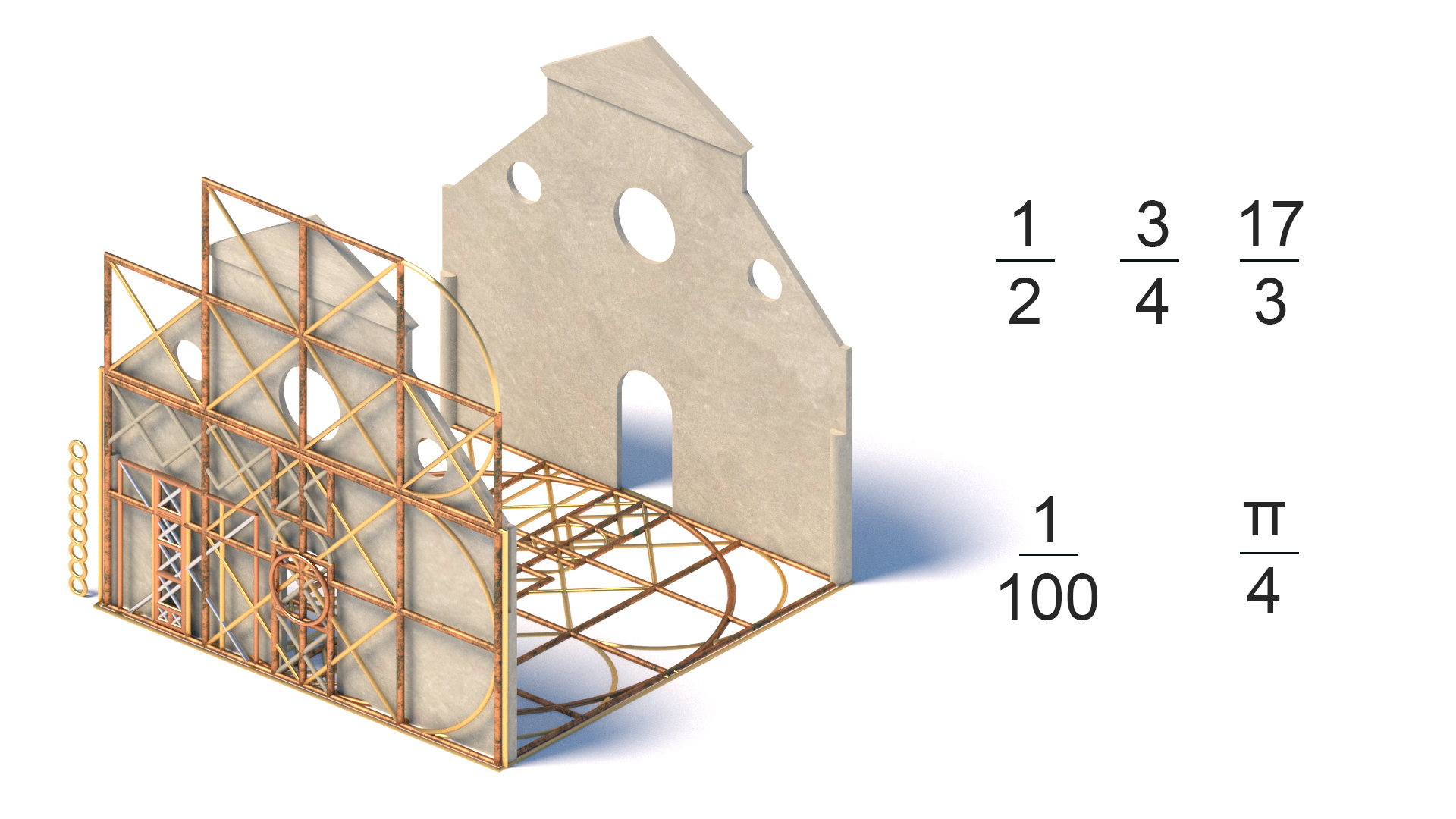
Brüche
Ein gebräuchlicher Dezimalpunkt (erfunden im 15. Gebäude und Kunst wurden in Bruchteilen dimensioniert, entweder die Multiplikation eines Moduls oder die Division des Ganzen. Einige davon würden zwei oder mehr Sätze von Basisfraktionen in derselben Arbeit enthalten. Dies ist eine der Kernmethoden in der klassischen Architektur Suche nach der idealen Geometrie, die fraktioniert geteilt werden könnte.
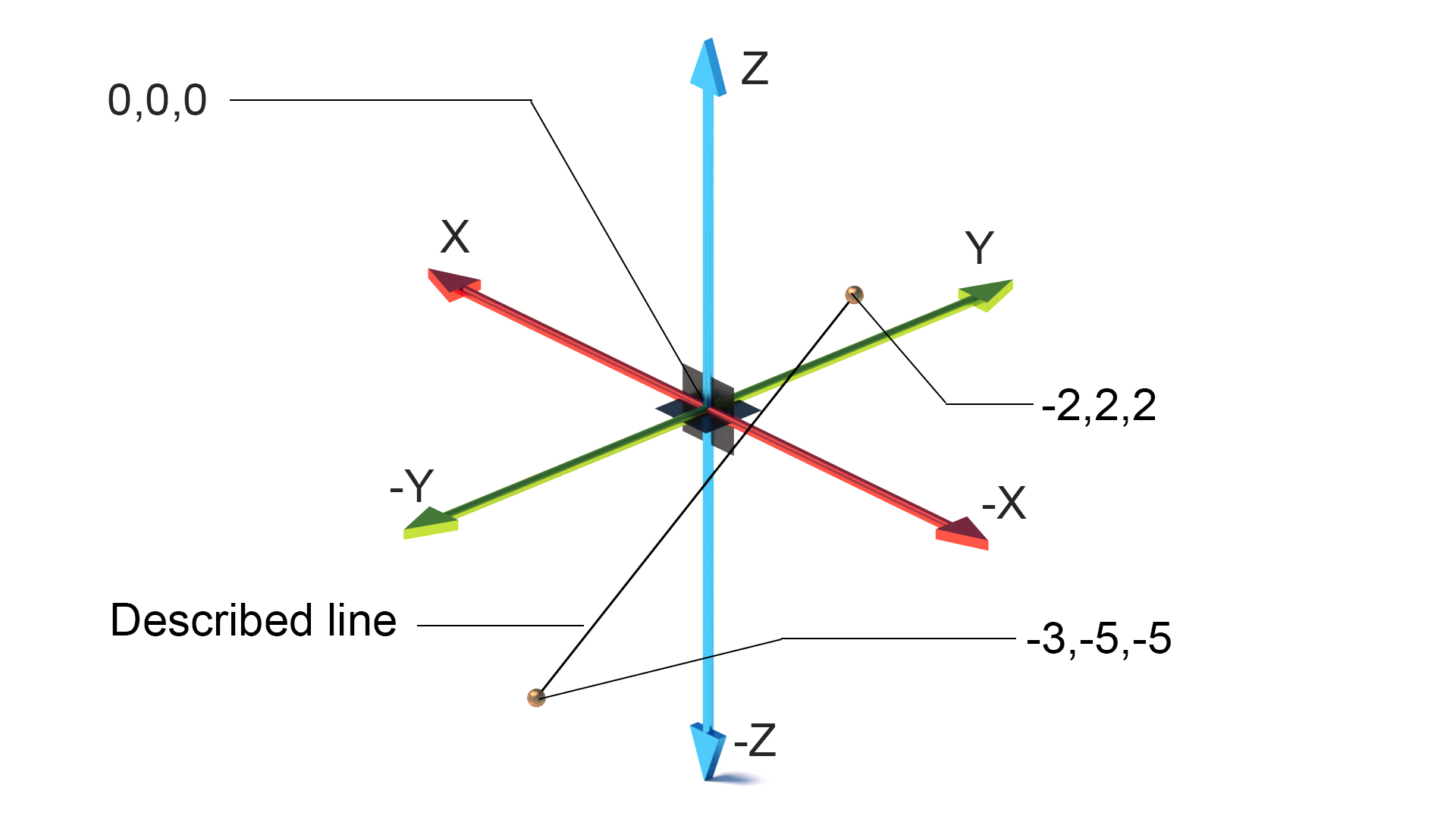
Kartesisches Koordinatensystem
Erfunden im 17. Descartes hatte die Idee, flache und dreidimensionale Formen in numerische Informationen umzuwandeln, die eine genaue Beschreibung der Welt mit mathematischen Mitteln ermöglichen.
In der Ebene (flach)besteht das Koordinatensystem aus Punkten und gibt jeden Punkt eindeutig durch ein Paar numerischer Koordinaten an, die die Abstände zum Punkt von zwei festen senkrechten Linien (x und y im Computergebrauch) sind. Der Punkt, an dem sich die Achsen treffen / kreuzen, ist die Ursprungsebene 0,0.
In einem 3-dimensionalen Raum wird eine dritte Achse hinzugefügt (Z), um die Höhe im System anzugeben. Alle Linien treffen sich in der gleichen Ursprungsebene 0,0,0.
Vektoren können auch verwendet werden, um die Position eines Punktes in einem Winkel und Abstand vom Ursprungsplan oder einem anderen Punkt zu beschreiben.
Dieses Koordinationssystem bildet die Grundlage von Computer Aided Design Software und ist darauf aufgebaut, komplexere Geometrien zu beschreiben.