Klassisk matematikk er nært knyttet til klassisk geometri i arkitektur. Et emne jeg har diskutert i et tidligere innlegg her. Dette er ikke en komplett liste over metoder eller formler, men en enkel oversikt Over metodene Arkitekter brukte tidligere. For forenklingsformål utelukker vi strukturelle beregninger som er basert på materialer, skala og belastninger og derfor for brede for en enkel bloggpost.
Tradisjonelt brukt i matematikk
Selv om vi ofte refererer til dette som i fortiden, er det fortsatt en pågående tradisjon for klassisk arkitektur, både som dialekt og klassisisme. Den tradisjonelle bruken av matematikk kan forenkles til 4 områder:
- Strukturelle Beregninger
- Geometri og romlige former
- Danner Estetikk, eller tro på skjønnhet som kommer fra former; proporsjoner og symmetrier.
- Dekorasjoner av overflater og former i det romlige miljøet
Modernismen beveget seg bort fra Dette på mange måter, men en økende interesse for parametrisk arkitektur har igjen tent en interesse for matematikk og geometri i arkitektur. Dette har blitt beriket i post-kalkulus æra med beregning av miljømessige og funksjonelle parametere. Et emne som vil bli utforsket i et annet eget innlegg.
Strukturberegning er et betydelig emne og vil ikke bli dekket i detalj her. Tilstrekkelig å si at strukturell design utviklet seg fra estimering av materialegenskaper til en informert beregning før bygging. Et område eller Arkitektonisk teori» Materielle Kulturer » teoretiserer at en arkitektonisk kulturell vekst skjer når en tradisjonell byggemetode beveger seg fra ett materiale til et annet. Et eksempel er den klassiske vestlige arkitekturen som opprinnelig var tømmer, som deretter ble oversatt til stein. Elementene i klassisk arkitektur bærer fortsatt disse originale tredetaljer, nå brukt som rene dekorasjoner i stein. Skalaen og teknologien til de nye materialkomponentene vil naturligvis måtte endres i oversettelsen og skape en ny estetikk.
Geometri
mens geometri og romlige former er avledet fra matematikk, diskuterte jeg dette i et eget innlegg.
Gudene Eller Naturen
Natur og religion har alltid vært grunnleggende i utformingen av vårt miljø. Tidlige agrariske kulturer ville identifisere at naturen fulgte regler som kunne oversettes til matematikk, fra proporsjonale regler til fraktalisering for å nevne to. Dette ble tatt som et bevis for at universet ble designet av Gudene. Så naturlig vil tilbedelsesstedene måtte bruke disse «hellige» reglene. Disse reglene vil da diffundere til andre steder av makt og deretter inn i den generelle vernacular bruk.
den religiøse bruken av disse matematikkene har hatt en tendens til å ligge til grunn for et symbolsk uttrykk for gudfryktig design, mens verdslig bruk har vært mer representativ for naturen. Bruken av disse matematikk og geometrier har derfor svingt mellom disse metodene avhengig av tidens filosofi, med allot overlapping.

Gylden Seksjon/Forhold
To mengder med en rasjon til hverandre som er den samme som rasjonen av summen til den største av mengdene. Den gylne delen ble ansett som en kjerne estetisk form, på grunn av sin rikelig eksempel i naturen. Estetisk teori hevder at det er spesiell skjønnhet stammer fra at skjemaet er et «mellom» mellom en firkant og et rektangel.
Fra Klassiske greske templer Til Renessansekirker og corbusier fasader, dette er uten tvil den mest gjenkjennelige klassiske formelen i både generell geometri og bygningsdetaljer.
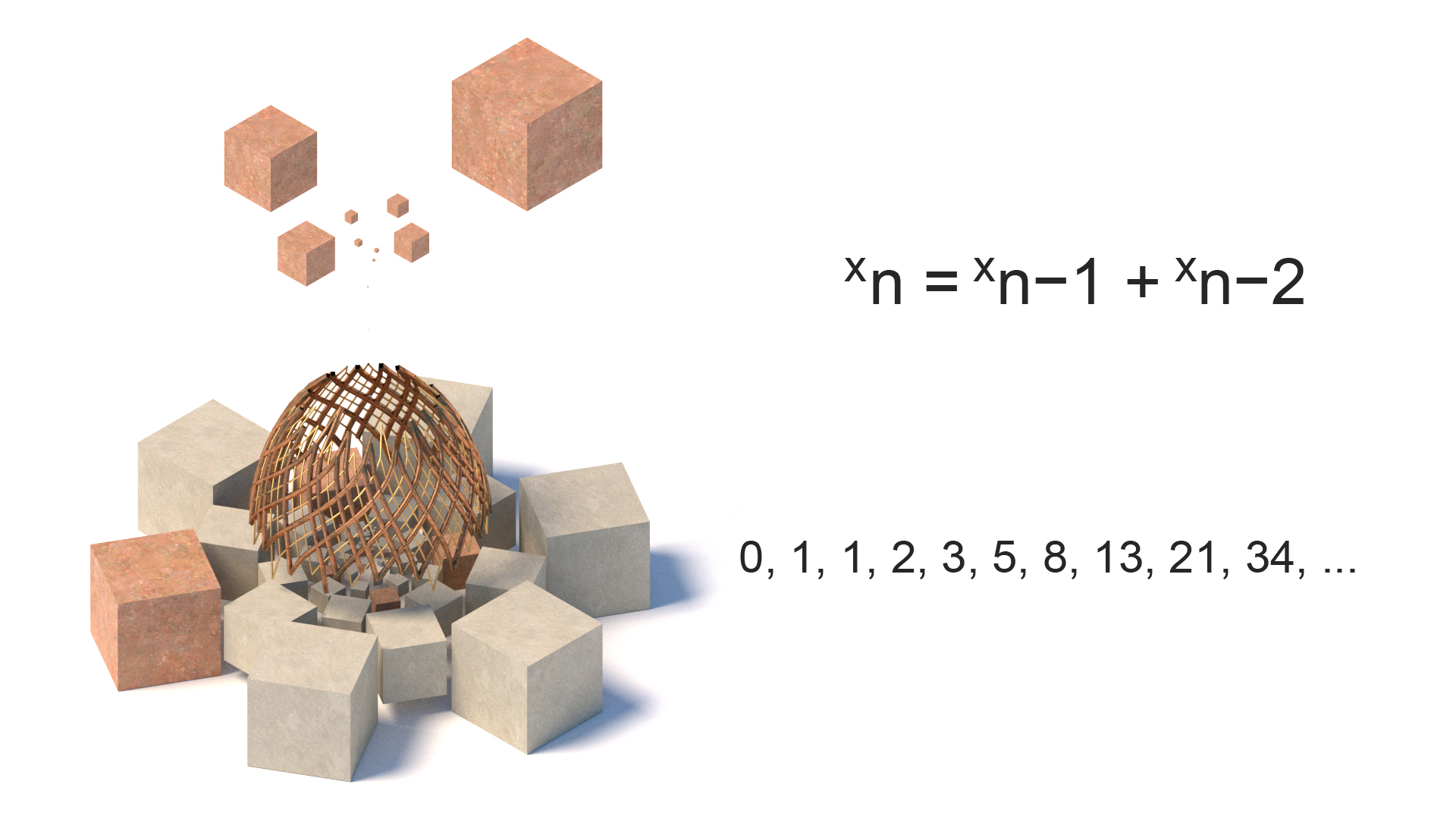
Fibonacci tall
Oppkalt etter den italienske matematikeren Leonardo I Pisa, Fibonacci-sekvensen er tall hvor hvert tall er summen av de to fortsetter tallene. Sekvensen hvis observert ofte i naturen som i tre forgrening, kongler etc. Bruken av dette i spiralformer kan bli funnet i alt fra klassiske greske templer Til Mona Lisa.
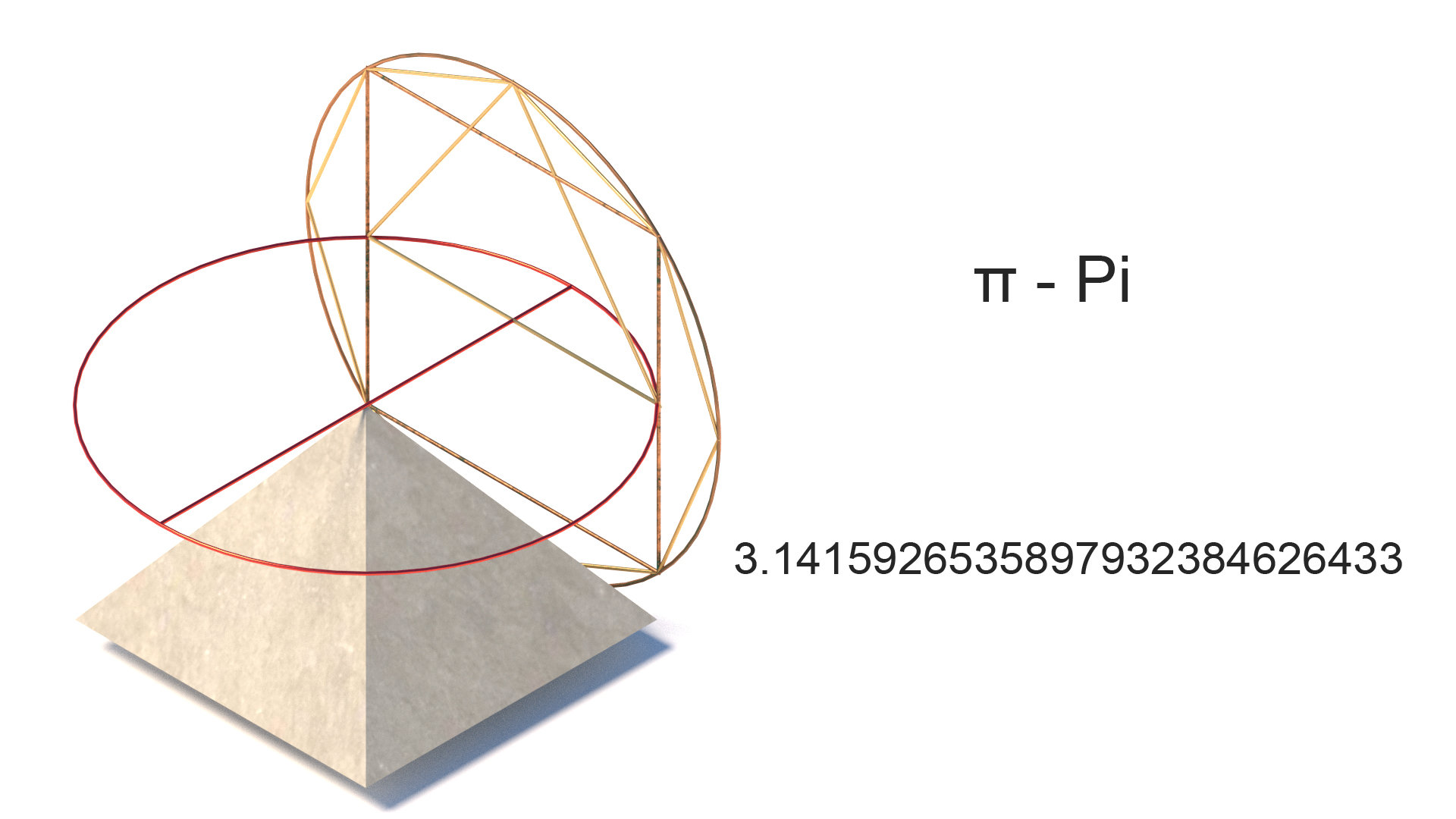
Pi π
Pi er fundamentalt forholdet mellom en sirkels omkrets og dens diameter og tilsvarer omtrent 3.14159. Representert av den greske «π» siden det 18. århundre. Mens pi er nyttig for å «kvadrere en sirkel» og beregne bruken av sirkulære former, har andre bruksområder blitt funnet fra fortiden. John Taylor (1859) oppdaget at hvis Omkretsen av Pyramiden er delt med høyden, er resultatet en nær tilnærming til 2 & pi .
Pi kan bidra til å måle ting som væske, lyd og lysbølger, og sannsynlighet som fordelingen av noder i moderne kalkulusbasert matte. Det er derfor kjernen i mange moderne parametriske beregninger.
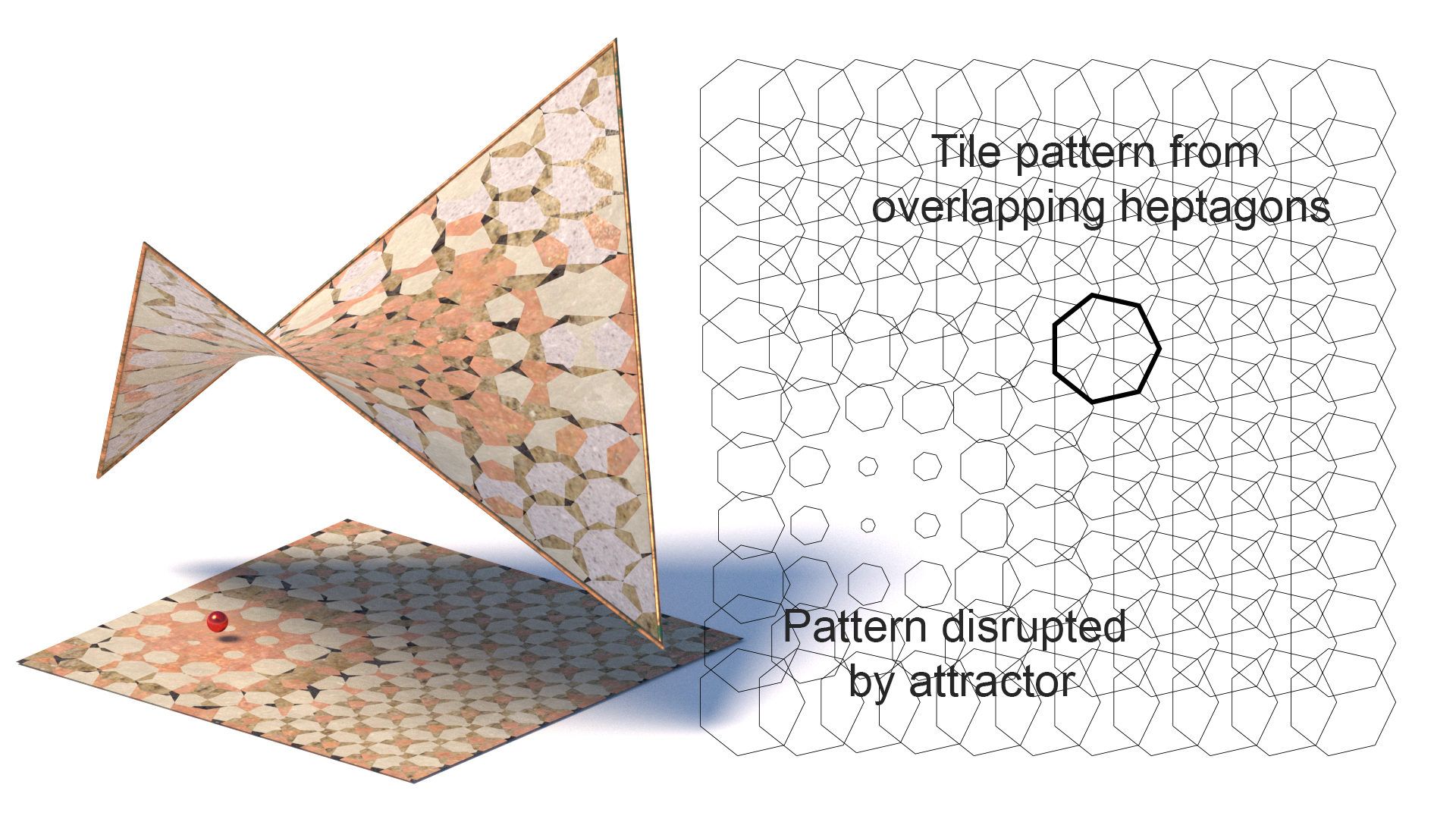
2d Og 3d Flislegging
Tessellasjon (flislegging)
Flislegging involvert dekker et plan overflate i geometriske figurer. Den enkleste inkluderer rektangulære fliser som ofte brukes i bad og kjøkken. Mer kompliserte former krever en mer komplekse metoder for repeterende geometrier. Den klassiske matematikken av repeterende mønstre var høyt utviklet I Midtøsten og Sørøst-Asia. Det er mange forskjellige former for tesselations, noen populære inkluderer:
- Vanlig tessellasjon er en kant til kant symmetrisk flislegging.
- Semi-regulær /Arkimedisk tessellasjon bruker mer enn en type regulær polygon i et isogonalt arrangement
- Monohedral flislegging er en tessellasjon der alle fliser har samme form og størrelse.
- Isohedral flislegging Er en spesiell variant av en monohedral flislegging der alle fliser tilhører samme transitivitetsklasse
- Voronoi /Dirichlet fliser Er tessellasjoner hvor hver flis er definert som settet av punkter nærmest et av punktene i et diskret sett med definerende punkter.
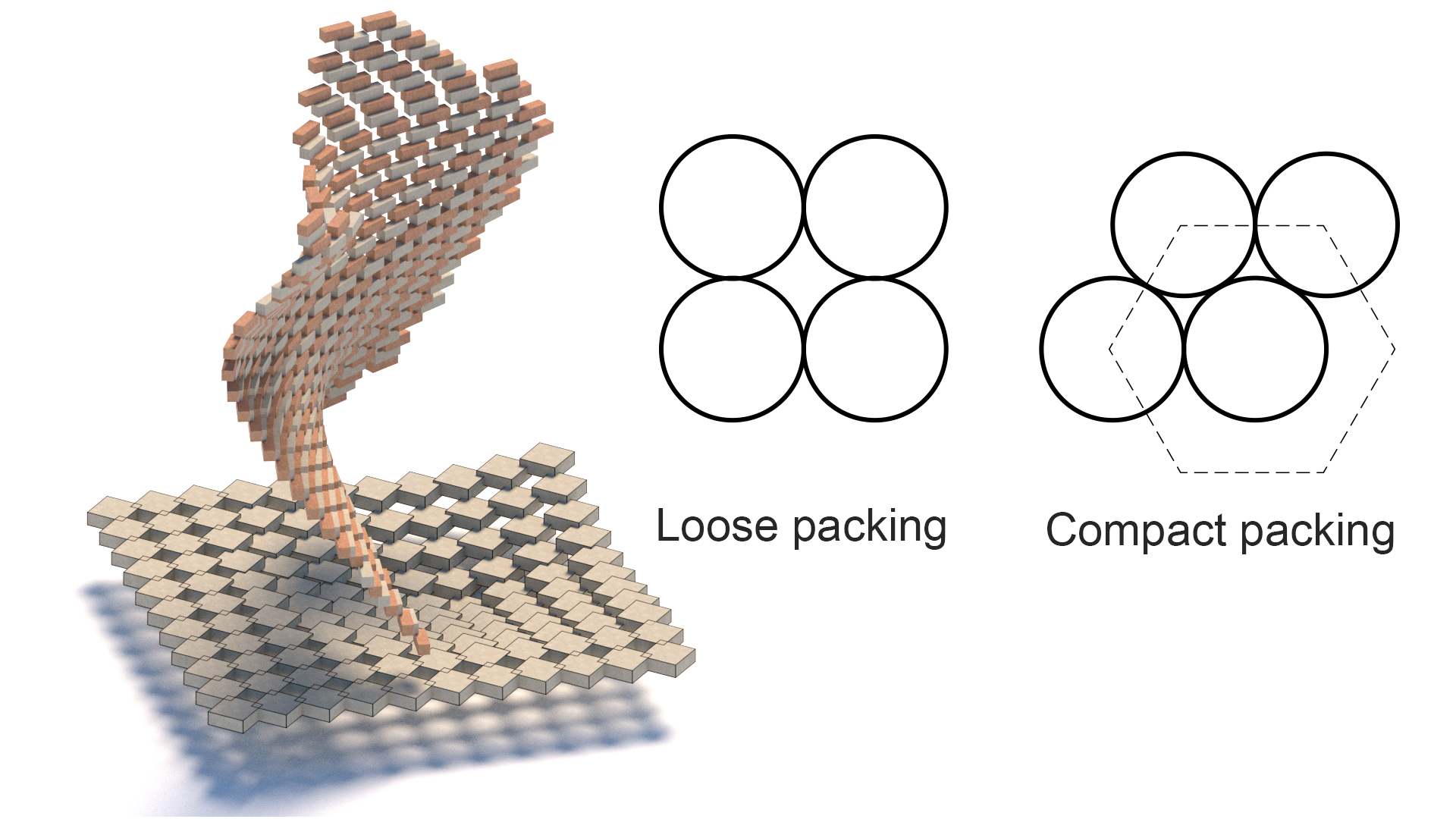
Klassisk Arkitektur pakking
Pakking
en versjon Av Tessellasjon, pakking innebærer stabling og sammenføyning av 3-dimensjonale enheter i et sammenhengende mønster med et variert tetthetsnivå.
et pakkeproblem inneholder to variabler:
- en ‘beholdere’; vanligvis en enkelt to-eller tredimensjonal region, eller et uendelig mellomrom
- et sett med ‘objekter’ som skal pakkes inn i en eller flere beholdere. Settet kan inneholde objekter i forskjellige størrelser, eller et enkelt repeterbart objekt med en fast dimensjon gjentatte ganger.
den matematiske modellen vil avhenge av formen til hver av disse variablene.
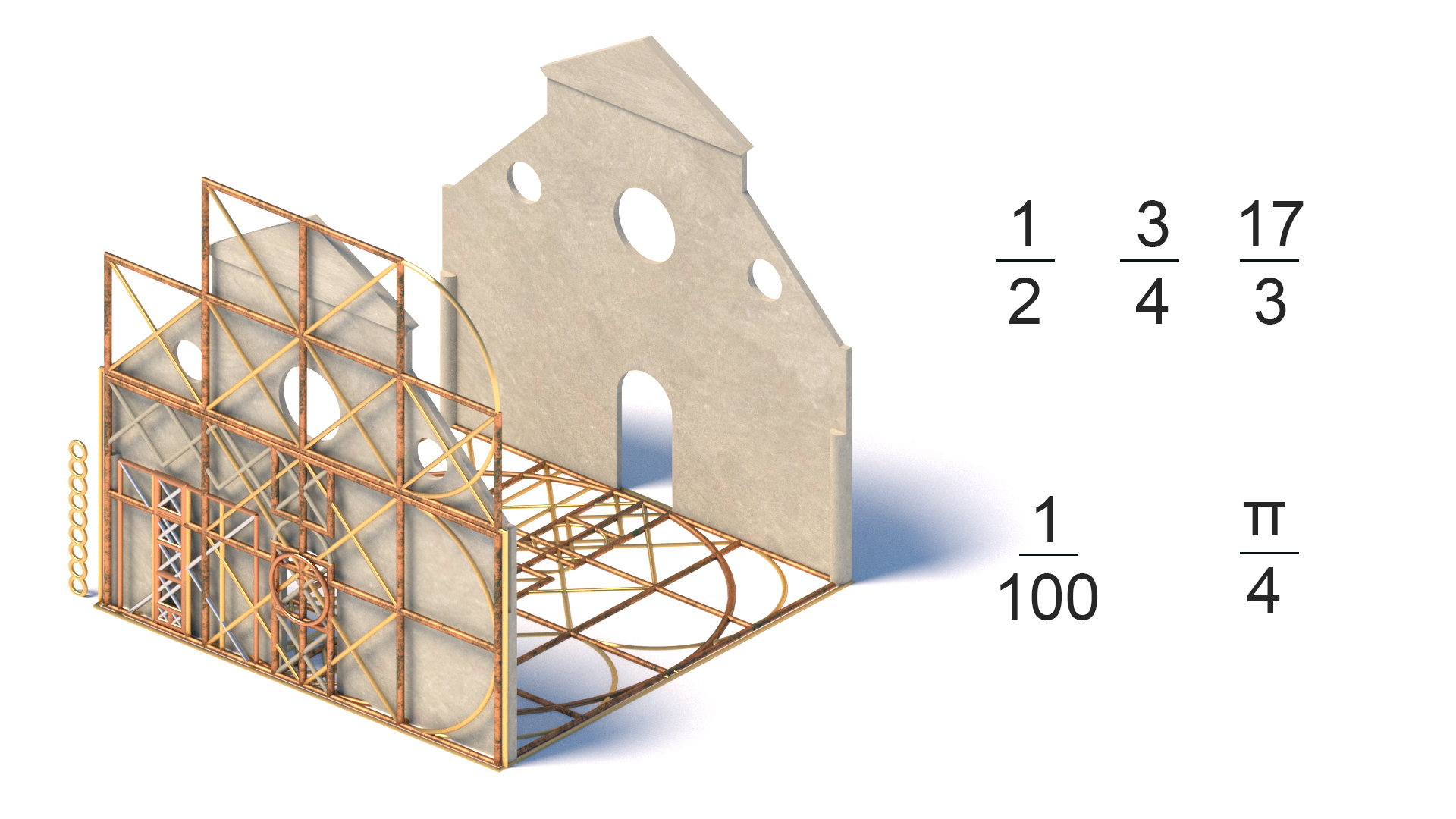
Fraksjoner
en vanlig bruk pre-desimalpunkt (oppfunnet i det 15. Århundre). Bygninger og kunst ble dimensjonert i form av fraksjoner, enten multiplikasjon av en modul, eller delingen av helheten. Somethimes disse vil inkludere to eller flere sett med basefraksjon i samme arbeid. Dette er en av kjernemetodene i den klassiske arkitekturens søk etter den ideelle geometrien som kan deles fraksjonalt.
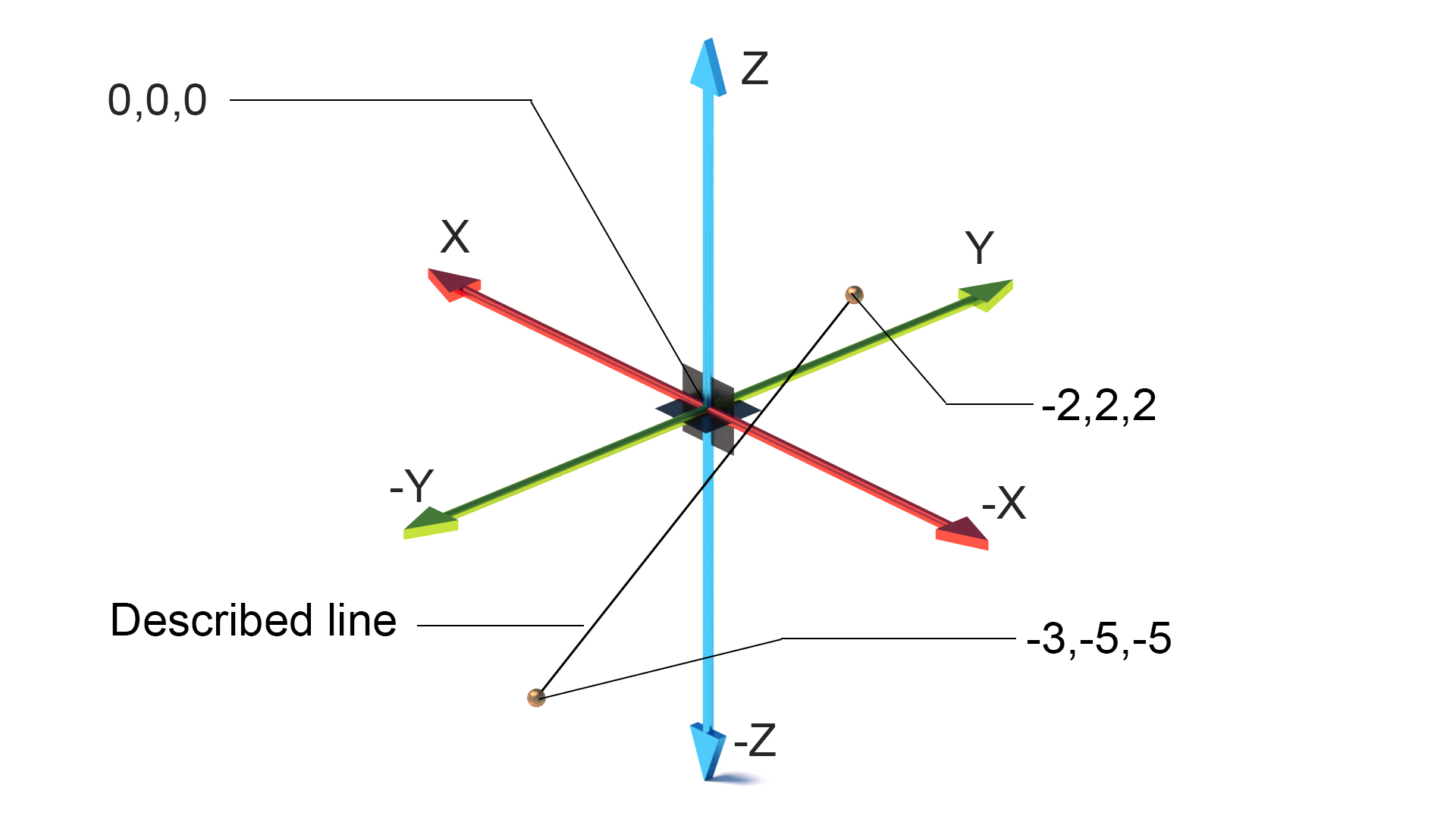
Kartesisk Koordinatsystem
Oppfunnet i det 17.århundre Av René Descartes av «jeg tror derfor jeg er» berømmelse. Descartes hadde ideen om å snu flate og tredimensjonale former til numerisk informasjon som ville tillate nøyaktige beskrivelser av verden gjennom matematiske midler.
i planet (flat) koordinatsystemet består av punkter og angir hvert punkt unikt ved et par numeriske koordinater som er avstandene til punktet fra to faste vinkelrette linjer( x og y i datamaskinbruk), disse referanselinjene kalles en koordinatakse av systemet. Punktet hvor aksene møtes / krysser er opprinnelsesplanet 0,0.
i et 3-dimensjonalt rom legges en tredje akse (Z) for å gi høyden i systemet. Alle linjene møtes på samme opprinnelsesplan 0,0,0.
Vektorer kan også brukes til å beskrive plasseringen av et punkt i en vinkel og avstand fra opprinnelsesplanen eller et annet punkt.
dette koordineringssystemet danner grunnlaget for datastøttet designprogramvare og er bygget på for å beskrive mer komplekse geometrier.